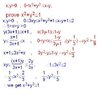Ask for hint for problem of inequality

[anemone]

Problem:

Let x and y be positive real numbers satisfying the inequality $\displaystyle x^3+y^3\le x-y$.

Prove that $\displaystyle x^2+y^2\le 1$ .

Hi all, I'm at my wit's end to prove the question as stated above, and I know it's obvious that $\displaystyle x-y>0$ and $\displaystyle x\ne1,\,y\ne1$, and if I factorized the LHS of the given inequality, I get:

$\displaystyle (x+y)(x^2-xy+y^2)\le x-y$

Now, since $\displaystyle x+y>0$, divide the left and right side by $\displaystyle x+y$ to get:

$\displaystyle x^2-xy+y^2\le\frac{x-y}{x+y}$

$\displaystyle x^2+y^2\le\frac{x-y}{x+y}+xy$

$\displaystyle x^2+y^2\le\frac{x-y+xy(x+y)}{x+y}$

And up to this point, I see no credible path to finish what I've started and I must be missing something very important here...

As usual, any guidance or help with this problem would be much appreciated.(Smile)

Thanks.

 

[Dustinsfl]

$$
\frac{x - y}{x + y} \leq 1
$$
So $x^2 + y^2 \leq 1 + xy$ .

Theorem:
Given real numbers $a = x^2 + y^2$ and $b = 1$ such that
$$
a\leq b + \varepsilon,\quad \forall\varepsilon > 0.
$$
Then $a\leq b$.

 

[anemone]

$$
\frac{x - y}{x + y} \leq 1
$$
So $x^2 + y^2 \leq 1 + xy$ .

Theorem:
Given real numbers $a = x^2 + y^2$ and $b = 1$ such that
$$
a\leq b + \varepsilon,\quad \forall\varepsilon >0
$$
Then $a\leq b$.

Thank you so much for answering to my question, but, I understand that the theorem is true iff $\varepsilon $ is small , and how do we know we have a small value of xy in this case?

 

[Dustinsfl]

Thank you so much for answering to my question, but, I understand that the theorem is true iff $\varepsilon $ is small , and how do we know we have a small value of xy in this case?

Suppose on the contrary that $b<a$, then let $\varepsilon = \frac{a - b}{2}$ (which may not be infinitesimal small).
$$
b + \varepsilon = b + \frac{a - b}{2} = \frac{a + b}{2} < \frac{a + a}{2} = a
$$
which is a contradiction.
Therefore, $a\leq b$.

 

[Albert1]

View attachment 559

 

[Dustinsfl]

View attachment 559

Let $x=y=\frac{1}{2}$.
$$
0\leq\frac{3}{4}\leq\frac{17}{16}\leq 1\leq 2
$$
which isn't true.
Also, x and y can be any real number it says in post 1.

 

[Albert1]

x,y are positive real numbers
$ x^3 +y^3 >0 $
$ so\,\, x\neq y$ (in fact x>y)
x,y be real numbers and meet the given restriction ,so at first I find the range of x and y then prove it will satisfy the inequility
(it is clear x,y can't be any real numbers)

 

[Dustinsfl]

x,y are positive real numbers
$ x^3 +y^3 >0 $
$ so\,\, x\neq y$ (in fact x>y)
x,y be real numbers and meet the given restriction ,so at first I find the range of x and y then prove it will satisfy the inequility
(it is clear x,y can't be any real numbers)

Pick up Tom Apostles Real Analysis book. The theorem I stated was for all real numbers not just less than 1

 

[anemone]

Here is another method to prove the inequality \(\displaystyle x^2+y^2 \le1\) given \(\displaystyle x^3+y^3\le x-y\) for all real $x$ and $y$. I just saw this solution from another site and immediately wanted to add that solution here...

\(\displaystyle x^3+y^3\le x-y\) tells us \(\displaystyle 0\le y \le x\).

Thus, we have \(\displaystyle x^3\le x\) and this implies \(\displaystyle x \le 1\) and \(\displaystyle 0\le y \le x \le 1\).

In particular, \(\displaystyle x(x+y) \le 1(2) \le 2\;\;\rightarrow\;\;xy(x+y) \le 2y\).

Finally, \(\displaystyle x^3+y^3=(x+y)(x^2-xy+y^2) \le x-y\), so

\(\displaystyle x^2-xy+y^2 \le \frac{x-y}{x+y}\)

\(\displaystyle x^2+y^2 \le \frac{x-y}{x+y}+xy \le \frac{x-y+xy(x+y)}{x+y} \le \frac{x-y+2y}{x+y} \le 1\). (Q.E.D.)