ASVAB circle and inscribed rectangle area problem

[karush]

Rectangle ABCD is inscribed in the circle shown.
If the length of side $\overline{AB}$ is 5 and the length of side $\overline{BC}$ is 12
what is the area of the shaded region?

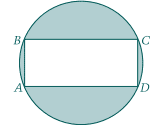
$a.\ 40.8\quad b.\ 53.1\quad c\ 72.7\quad d \ 78.5\quad e\ 81.7$

well to start with the common triangle of 12 5 13 gives us the diameter of 13
area of the circle is $\pi \left(\frac{13}{2}\right)^2=132.73$
area of {circle - retangle)=$132.73-60 =72.7$ which is c

typos maybe:unsure:

 

[skeeter]

assuming $\overline{BC} = 12$, not $\overline{AB}$

$\pi \left(\dfrac{d}{2}\right)^2 - |AB| \cdot |BC|$

 

[HOI]

I, because of my "prejudices", would immediately go to coordinate methods. Set up a Cartesian coordinate system with center at the center of the circle and with axes parallel to the sides of the rectangle.

The circle can be written $x^2+ y^2= R^2$. The line AB is x= -6 and CD is x= 6. The line BC is y= 5/2 and the line AD is y= -5/2.

The line y= 5/2 intersects the circle where $x^2+ 25/4= R^2$, so $x^2= R^2- 25/4$- that is at $\left(\sqrt{R^2- 25/4}, 5/2\right)$.
The line x= 6 intersects the circle where $36+ y^2= R^2$, so $y^2= R^2- 36$- that is at $\left(6, \sqrt{R^2- 36}\right)$.

Of course, those refer to the same point so we must have $6= \sqrt{R^2- 25/4}$ and $5/2= \sqrt{R^2- 36}$. The first is equivalent to $36= R^2- 25/4$ and the second to $25/4= R^2- 36$ so both give $R^2= 36+ 25/4= (144+ 25)/4= 169/4$ so $R= \pm\frac{13}{2}$. Since the radius of this circle is a positive number, $R= \frac{13}{2}$.

The circle has radius $\frac{13}{2}$ so area $\frac{169\pi}{4}$. The area of the rectangle is $12(5)= 60$ so the area of the shaded region is $\frac{169\pi}{4}- 60= \frac{169\pi- 240}{4}$.

 

[karush]

well this would be a lot easier if it wasn't decimal

 

[karush]

assuming $\overline{BC} = 12$, not $\overline{AB}$

$\pi \left(\dfrac{d}{2}\right)^2 - |AB| \cdot |BC|$

not sure if I have seen this notation before: |AB| as a distance between?

 

[skeeter]

not sure if I have seen this notation before: |AB| as a distance between?

yes

 

[karush]

Jolly Good Mate!