Asymptote of x^3 - x^5 / ( x^2 + 1) and similar curves

[Swamp Thing]

Playing with some numerical simulations, I plotted this in Wolfram Cloud / Mathematica:
$x^3-\frac{x^5}{x^2+2}$

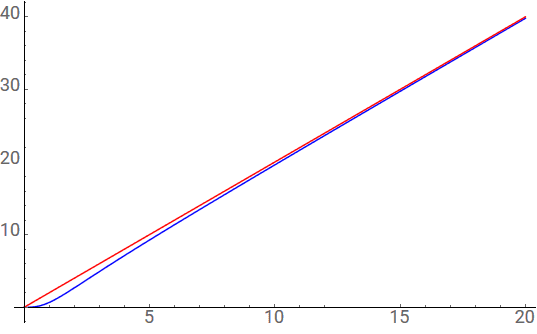
I had naively expected it to approach $x^3−x^3=0$, but that isn't the case. It approaches 2x.
I can now vaguely understand that the two terms need not cancel at infinity, but I'd like to get a better handle on this.

[1] How to break this down intuitively and estimate the qualitative nature of the asymptote "by inspection"?

[2] How can we obtain the asymptote $2x$ theoretically?

[3] Can we find the equation of the asymptote using Mathematica etc?

[Moderator's note: Moved from a technical forum and thus no template.]

 

[fresh_42]

$x^3 -\dfrac{x^5}{x^3+2} \sim x^3 -x^{5-3} = x^3 -x^2 \sim x^3$ although it looks as if you used another scaling.

 

[Swamp Thing]

Sorry, the laTex formula was wrong. I've corrected it. It has $x^2$ in the denominator.

Plot[{x^3-x^5/(x^2+2),2*x},{x,0,20},ImageSize->600,AxesStyle->20,PlotStyle->{Blue,Red},PlotRange->All]

Corrected the title as well.

 

[fresh_42]

Then use good old basic fraction algebra! Search a common denominator, expand the first fraction, add them, calculate the new numerator, divide again and see what the leading term is. Where is the problem?

 

[Swamp Thing]

Silly me.

 

[Mark44]

$x^3-\frac{x^5}{x^2+2} = \frac{x^3(x^2 + 2) - x^5}{x^2 + 2} = \frac{x^5 + 2x^3 - x^5}{x^2 + 2} = \frac {2x^3}{x^2 + 2}$
If you carry out the polynomial division, you get 2x plus a proper rational expression.

Whenever you have a rational function, as in the third expression above, where the degree of the numerator is one more than the degree of the denominator, there will be a slant asymptote. In this case, the slant asymptote is the line y = 2x, which is what you're seeing in the Wolfram graph.