- #1
m4r35n357
- 654
- 148
- TL;DR Summary
- Deathmatch
I thought I would give you guys some justification for why I keep pestering you with this odd numerical technique. I've mentioned its advantages over finite differences quite a few times, so now I am putting it up against symbolic differentiation.
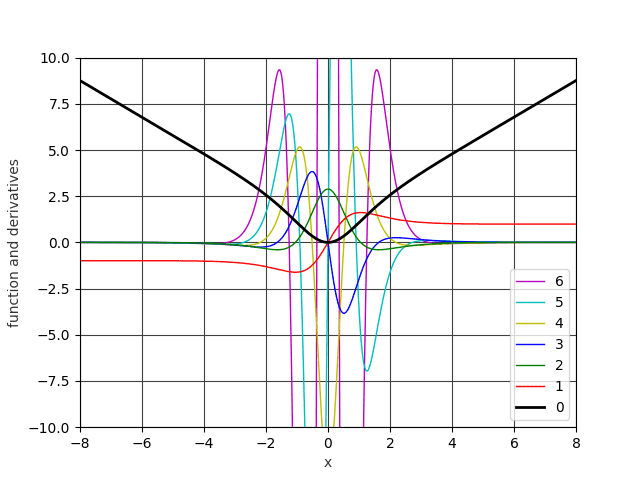
Here is a plot of the function ##x^2 / {\ln(\cosh(x) + 1)}##, together with its first six derivatives, using automatic differentiation (1001 x data points in total). The computations use 236 bit floating point precision courtesy of gmpy2 (MPFR) arbitrary point arithmetic.
Here is an illustration of the CPU time involved in generating the data:
Here is an interactive session evaluating the same function at a single point, ##x = 2##, together with its first twelve derivatives:
Finally, for comparison, here is something to cut & paste into Wolfram Alpha (symbolic computation):
I couldn't get it to do the twelfth derivative, and even for the sixth it will not attempt to evaluate the value (not unless I register anyway!).
Enjoy!
Here is a plot of the function ##x^2 / {\ln(\cosh(x) + 1)}##, together with its first six derivatives, using automatic differentiation (1001 x data points in total). The computations use 236 bit floating point precision courtesy of gmpy2 (MPFR) arbitrary point arithmetic.
Here is an illustration of the CPU time involved in generating the data:
Code:
$ time -p ./models.py 0 -8 8 1001 7 1e-12 1e-12 > /tmp/data 2>/dev/null
real 0.30
user 0.29
sys 0.00
Code:
$ ipython3
Python 3.7.1 (default, Oct 22 2018, 11:21:55)
Type 'copyright', 'credits' or 'license' for more information
IPython 7.2.0 -- An enhanced Interactive Python. Type '?' for help.
In [1]: from ad import *
ad module loaded
In [2]: x = Series.get(13, 2).var
In [3]: print(~(x * x / (x.cosh + 1).ln))
+2.562938002e+00 +1.312276410e+00 -3.440924889e-01 +2.366685634e-01 +2.260914151e-01 -1.617592557e+00 +5.097273067e+00 -1.157769456e+01 +1.290979888e+01 +5.759642561e+01 -5.363560778e+02 +2.667773442e+03 -8.844486444e+03
Code:
d^6/dx^6 x^2 / ln(cosh(x) + 1) where x = 2Enjoy!
Last edited: