Average distance to surface of sphere

[Opus_723]

Homework Statement

First, the problem, quoted verbatim:

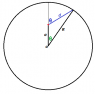
"Neutrons are created (by a nuclear reaction) inside a hollow sphere of radius R. The newly created neutrons are uniformly distributed over the spherical volume. Assuming that all directions are equally probable (isotropy), what is the average distance a neutron will travel before striking the surface of the sphere? Assume straight line motion, no collisions."

The problem then has several "steps" to help you along. I'm stuck on the first one, setting up the integral,

$\bar{r}=3R/2\int^{1}_{0}\int^{\pi}_{0}\sqrt{1-k^{2}sin^{2}\theta}*k^{2}sin\theta*dk*d\theta$

The Attempt at a Solution

I've mostly got it, except that my expression under the square root is wrong, so I think I'm having a conceptual issue with how to calculate the average distance. I found the distance from a point within the sphere at distance a from the orgin on the z-axis to a given point on the sphere using the law of cosines:

d=$\sqrt{R^{2}+a^{2}-2Racos\theta}$

Using this distance, I integrated over theta, phi, and a, then divided by the volume of the sphere. After substituting Rk = a, I got:

$\bar{r}=3R/2\int^{1}_{0}\int^{\pi}_{0}\sqrt{1+k^2-2kcos\theta}*k^{2}sin\theta*dk*d\theta$

So clearly I'm making a mistake with the distance. Could someone set me straight?

 

[TSny]

I believe that the angle $\theta$ in the expression $\bar{r}=3R/2\int^{1}_{0}\int^{\pi}_{0}\sqrt{1-k^{2}sin^{2}\theta}*k^{2}sin\theta*dk*d\theta$ is the blue angle $\theta$ as shown in the attached figure (rather than the green angle $\small \theta$ shown).

Your expression $d=\sqrt{R^{2}+a^{2}-2Racos\theta}$ is in terms of $\theta$.

What expression do you get for $d$ in terms of $\theta$, $R$, and $k$?

 

[Opus_723]

Wow! Thanks, I never would have thought of that. And it makes me feel a little better knowing I wasn't completely off.

I didn't see any real clean way to find the distance using that angle, but I managed to make do with a right triangle and the quadratic formula. If you know of a nicer way to see it, I'd be interested.

But what I found using your angle is that the distance d is equal to:

$-a*cos\theta+\sqrt{R^{2}-a^{2}sin^{2}\theta}$

And it looks like when you integrate that over theta from 0 to $\pi$ like in my original integral, the term outside the square root disappears (since adding the volume element gives us sinθcosθ), and leaves you with the expression found in my book.

Does that sound right? Out of curiosity, how did you know to look at that angle? Is that common?

 

[TSny]

I didn't see any real clean way to find the distance using that angle, but I managed to make do with a right triangle and the quadratic formula. If you know of a nicer way to see it, I'd be interested.

But what I found using your angle is that the distance d is equal to:

$-a*cos\theta+\sqrt{R^{2}-a^{2}sin^{2}\theta}$

Yes, that looks right. Initially I used the law of cosines in the form $R^2 = a^2 + d^2 + 2ad cos\theta$ and then solved for d using the quadratic formula. Geometrically, you can use the attached figure where you can see that $d + a cos \theta = \sqrt{R^2-a^2 sin^2 \theta}$. Maybe this is similar to what you did.

And it looks like when you integrate that over theta from 0 to $\pi$ like in my original integral, the term outside the square root disappears (since adding the volume element gives us sinθcosθ), and leaves you with the expression found in my book.

Does that sound right? Out of curiosity, how did you know to look at that angle? Is that common?

Yes, that sounds right.

The reason for using the angle θ as defined here is because the neutron has the same probability of moving away from its initial point in any direction. So, the probability that the neutron travels away between $\theta$ and $\theta + d\theta$ and azimuthal angle $\phi$ and $\phi + d\phi$ is $(1/4\pi) sin \theta \: d\theta \: d\phi$. Integrating this over all azimuthal angles $0 < \phi < 2 \pi$ gives $(1/2)sin\theta \: d\theta$ for the probability of heading out between $\theta$ and $\theta + d\theta$ for all azimuthal angles $\phi$. This is how the $(1/2)sin\theta \:d\theta$ ends up appearing in the integral.

If you measure the angle $\Theta$ from the center of the sphere, then the expression for the probability that the neutron (at distance $a$ from the center) heads out between $\Theta$ and $\Theta + d\Theta$ is a much more complicated function of $\Theta$.

 

[heritage972]

Actually had something to say but Latex here is beyond me. I write articles with LaTex in TeXworks but am at a complete loss here. Sorry. I tried to post something but can't delete it.

 

[haruspex]

I think the integration is easier if you turn the problem on its head. All exit points are equally likely, so instead you can ask the average distance from a fixed point P on the surface to points in the interior.
If the sphere is radius R, consider the points distance r from P. These form a spherical cap. The cap subtends an angle $2\alpha$ at P, $r=2R\cos(\alpha)$. The area of the cap is $2\pi r^2(1-\cos(\alpha))$. Substituting to eliminate $\cos(\alpha)$ we get an easy integral in r.