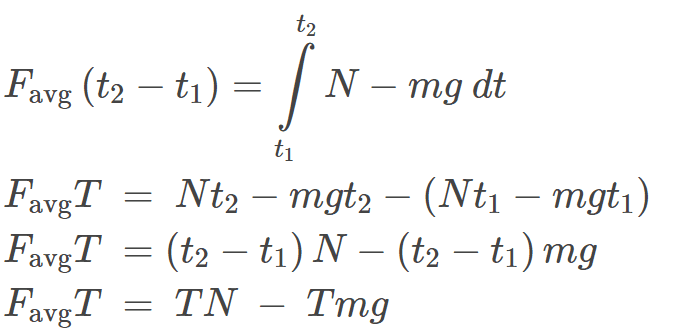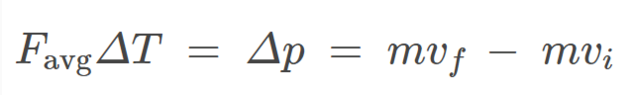Homework Help Overview
The discussion revolves around calculating the average force exerted by a bouncy ball during its collision with a surface. The problem involves concepts from dynamics and kinematics, particularly focusing on forces acting during the contact period and the implications of height changes on velocity.
Discussion Character
- Exploratory, Assumption checking, Conceptual clarification
Approaches and Questions Raised
- Participants explore the correct formulation of the average force equation, questioning the treatment of the normal force and gravitational force in the integral. There are discussions about using kinematic equations to relate initial and final heights to the average force, and some participants express uncertainty about how to incorporate these heights into their calculations.
Discussion Status
The discussion is active, with participants providing hints and guidance on how to approach the problem. There is a recognition of the need to clarify the average force over the contact time specifically, and some participants are attempting to derive expressions for change in momentum and average force based on the information provided.
Contextual Notes
There is mention of ambiguity regarding the definition of the time average, specifically whether it should be over the contact duration or the entire process. Additionally, participants note the importance of using the heights information and the implications of the impulse-momentum relationship in their reasoning.