Backward Euler technique vs. periodic function: Damping out?

[maistral]

So I've been programming the BDF methods and for some reason I have an issue with the Backward Euler technique.

Given the differential equation y" + y = 0 (with y(0) = 2, y'(0) = 0), my backward Euler solution goes like this:

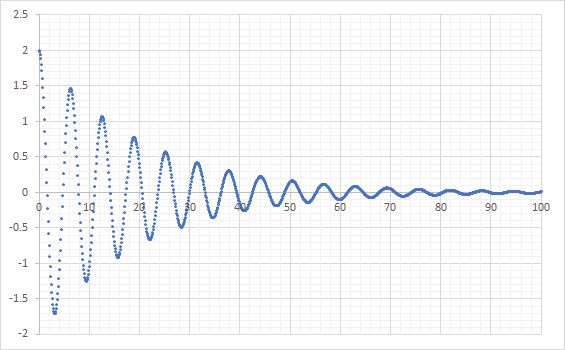
Obviously this is not possible as the function should be a well-behaved periodic. So I tried running my BDF2 and BDF4 on it, and this happens:

So yeah. What the actual flying . I have had this issue since about a week and a half now and I am running out of ideas. I made sure that my backward Euler code isn't the problem as I used test functions from different literature like those in Chapra and such other examples available; and the results from my code and those in examples are practically identical to the last digit in those examples.

What's stranger is the fact that I used the same Backward Euler code in order to generate the initial points for BDF2/BDF4! I am totally confused and appalled.

Is there something with the backward Euler and periodic functions that I am missing?

 

[pasmith]

In this case, the backwards Euler method with timestep h yields <br /> \begin{pmatrix} 1 &amp; -h \\ h &amp; 1 \end{pmatrix}\begin{pmatrix} u_{n+1} \\ v_{n+1} \end{pmatrix} =<br /> \begin{pmatrix} u_n \\ v_n \end{pmatrix} where u_n = y_n and v_n = y_n&#039;. The eigenvalues of the matrix on the left are 1 \pm ih, so their reciprocals both have magnitude (1 + h^2)^{-1/2} &lt; 1 for any positive h. Thus |u_n| \to 0.

 

[pasmith]

An alternative approach is to integrate once to obtain <br /> y&#039; = \pm \sqrt{y(0)^2 + y&#039;(0)^2 - y^2} and solve that instead (remembering that you have to change signs whenever y&#039; = 0).

 

[pasmith]

Finally: solving the recurrence relation yields <br /> \begin{pmatrix} u_n \\ v_n \end{pmatrix} = (1 + h^2)^{-n/2} \begin{pmatrix} \cos n\alpha &amp; -\sin n \alpha \\<br /> \sin n \alpha &amp; \cos n\alpha \end{pmatrix} \begin{pmatrix} u_0 \\ v_0 \end{pmatrix} where <br /> \cos \alpha = \frac{1}{\sqrt{1 + h^2}}. For (u_0, v_0) = (1,0) this yields <br /> u_n = \frac{\cos n\alpha}{(1 + h^2)^{n/2}} as compared with the exact \cos nh. You can see that the amplitude decays and the phase shifts.

 

[pbuk]

Is there something with the backward Euler and periodic functions that I am missing?

Yes: first order methods perform badly on periodic functions. In general, explicit methods explode to infinity and implicit methods decay to zero (you can see this from the sign of the truncated $f''$ error term), and @pasmith has provided an execellent analysis for this particular problem.

Where are you learning about these methods from? If you are to use them successfully you can't skip the 'analysis' part of 'numerical analysis'.

 

[maistral]

I have a final question.

With respect to multistep methods I have noticed that some algorithms do variable-order approach. May I know the reason behind this? Why would you select Backward Euler over BDF4?

 

[pbuk]

Why would you select Backward Euler over BDF4?

Generally you wouldn't, but you can't select BDF4 over Backward Euler until you have already done 3 steps!

 

[maistral]

Generally you wouldn't, but you can't select BDF4 over Backward Euler until you have already done 3 steps!

No, what I mean is the variable step/variable order BDF/NDF which is typically used by programs like MATLAB. I don't quite understand why on Earth would you force the order to be lowered; I fully understand the vsriable step part but not the variable order part.