Baire Category Theorem .... Stromberg, Theorem 3.55 .... ....

[Math Amateur]

TL;DR

The post concerns an aspect of Stromberg's proof of the Baire Category Theorem ... ...

I am reading Karl R. Stromberg's book: "An Introduction to Classical Real Analysis". ... ...

I am focused on Chapter 3: Limits and Continuity ... ...

I need help in order to fully understand the proof of Theorem 3.55 on page 110 ... ...Theorem 3.55 and its proof read as follows:

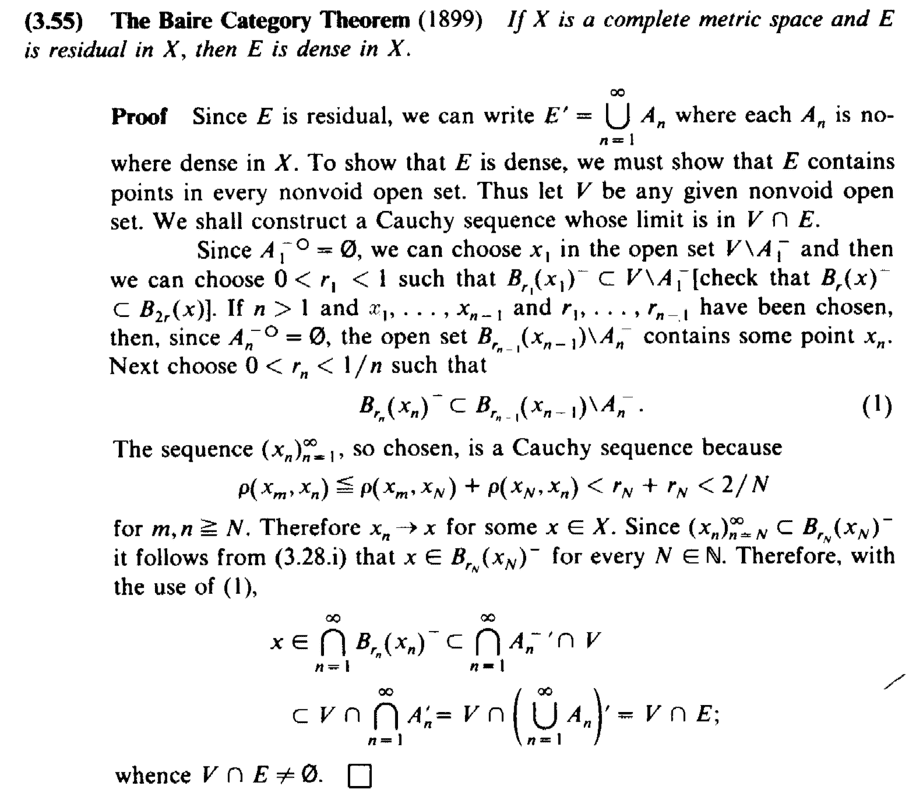At the start of the second paragraph of the above proof by Stromberg we read the following:

" ... ...Since $A_1^{ - \ \circ } = \emptyset$, we can choose $x_1$ in the open set $V$ \ $A_1^{ - }$ and then we can choose $0 \lt r_1 \lt 1$ such that $B_{ r_1 } ( x_1 )^{ - } \subset V$ \ $A_1^{ - }$ [ check that $B_r (x)^{ - } \subset B_{ 2r } (x)$ ] ... ...My questions are as follows:Question 1

Can someone explain and demonstrate exactly/rigorously why/how it is that $A_1^{ - \ \circ } = \emptyset$ means that we can choose $x_1$ in the open set $V$ \ $A_1^{ - }$ ... it seems very plausibly the case ... but ... how are we (rigorously) sure this is true ... ?
Question 2

How/why can we choose $0 \lt r_1 \lt 1$ such that $B_{ r_1 } ( x_1 )^{ - } \subset V$ \ $A_1^{ - }$ ... ?

... and why are we checking that $B_r (x)^{ - } \subset B_{ 2r } (x)$ ... ... ?

*** EDIT ***

My thoughts on Question 2 ...

Since $V$ \ $A_1^{ - }$ is open ... $\exists \ r_1$ such that $B_{ r_1 } ( x_1 ) \subset V$ \ $A_1^{ - }$ ...

... BUT ... how do we formally and rigorously show that ...

... we can choose an $r_1$ such that the closure of $B_{ r_1 } ( x_1 )$ is a subset of $V$ \ $A_1^{ - }$ ... ( ... intuitively we just choose $r_1$ somewhat smaller yet ... )

... and further why is Stromberg talking about $r_1$ between $0$ and $1$ ...?
Help will be much appreciated ...

Peter
==========================================================================================================================

The definitions of nowhere dense, first and second category and residual are relevant ... so I am providing Stromberg's definitions ... as follows:

Stromberg's terminology and notation associated with the basic notions of topological spaces are relevant to the above post ... so I am providing the text of the same ... as follows:

Hope that helps ...

Peter

 

[andrewkirk]

On the first one:

Assume the opposite: that V\A1- is empty. Then A1- contains V, which is a nonempty open set and has interior points (since all points in an open set are interior). So A1- has interior points, but it is the closure of A1, and that contradicts the statement that A1 is nowhere dense. From this contradiction we conclude that V\A1- cannot be empty.

 

[andrewkirk]

On the second one, note that V\A1- is open because it is the intersection of open set V with the complement of A1-, which is open because A1- is closed. Since it is open, all its points are interior and in particular x1 is, so there exists some h such that the ball Bh(x1) is contained in V\A1- .

He requires r1<1 because a little further down he requires that rn < 1/n. That's how he makes the sequence Cauchy.

 

[Math Amateur]

Thanks so much for the help, Andrew

Just working through your posts now ...

Thanks again,

Peter

 

[Math Amateur]

On the second one, note that V\A1- is open because it is the intersection of open set V with the complement of A1-, which is open because A1- is closed. Since it is open, all its points are interior and in particular x1 is, so there exists some h such that the ball Bh(x1) is contained in V\A1- .

He requires r1<1 because a little further down he requires that rn < 1/n. That's how he makes the sequence Cauchy.

Thanks again for the help Andrew ...

... but ... just a clarification ...

... how exactly do we demonstrate rigorously .. given the ball $B_h (x_1) \subset V$ \ $A_1^{ - }$

... we then have $B_h (x_1)^{ - } \subset V$ \ $A_1^{ - }$ ... ... ?Hoe you can help further ...

Peter

 

[andrewkirk]

Find an h' such that the open ball of radius h' is in that set. Then set h=h'/2. The closure of that ball will be inside the open ball of radius h' (as the closure is the set of points distant no further than h'/2 from the point, and that is a subset of the bigger open ball, set of points distance less than h' from the point), and hence will be in the required set.

This may relate to a tangential question you were asking earlier - something about checking the closures of balls with double or half the radius.