Ball in accelerating tank with fluid

[Epiclightning]

T1. Homework Statement
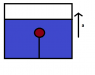
a wooden ball of mass m is kept inside water by the help of a massless string shown in the figure. One end of the string is fixed at the bottom of the vessel. when the vessel containing the water is accelerated upwards with acceleration a , will the tension increase and why?

Homework Equations

B = Vdg,
Vdg-mg-T = ma

The Attempt at a Solution

The answer is that the tension increases, but according to the equations above, buoyancy remains constant and the new tension is T = Vdg-mg-ma, which is lesser than before(Vdg-mg).

 

[Rx7man]

I look at it as the acceleration of the whole tank upwards is doing nothing other than changing gravity...

The tension on the string is proportional to the total acceleration of the system... if it's accelerating upward at 9.8m/s^2 there would be double the tension.

 

[haruspex]

Homework Equations

B = Vdg,

That equation is only valid if the medium is not accelerating. To make it more general, compare the forces on the wooden ball to the forces that would act on the ball of water it is displacing,