- #1
subhradeep mahata
- 120
- 13
Homework Statement
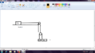
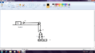
The figure shows three blocks with their masses m,2m and 3m and two pulleys. Assuming that the pulleys and strings are massless and ideal, calculate the tension in lower string and acceleration in 3m block.
Homework Equations
The Attempt at a Solution
We have to find T. Now, let's assume that the 2m block moves downwards with acceleration a, and the m block move upwards with acceleration a as well.
Accordingly,
2mg-T=2ma and T-mg=ma
adding them, we get a=g/3
substituting it in the first equation, T=4mg/3.
Also, 2T=3m * acc
On solving, we get acc =8g/9, which is acceleration of 3m block.
But, my book says that the product of tension of the segment of the string and the corresponding acceleration of the block is constant. But my answers don't seem to match this criteria.
Neither do i know the meaning of the statement or how it has been derived, nor can I find any mistake in my method(if there is any). Kindly please address the issue.