Ball suspended by a pulley: oscillation

[inv4lid]

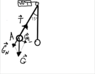
A ball of 100g, suspended from a pulley of a dynamometer, oscillates freely. The length of the pendulum thus obtained is 1m. What are the indications of the dynamometer when the ball is at the point A of it's trajectory? The maximum offset angle is 15 degrees.

Homework Equations

α - alpha (angle), G - gravity, T - restoring force[/B]
m= 0,1 kg.
l = 1m.
α = 15 degrees
_________________|
Sum of all forces (probably, not sure)

Attempts of solving:

If I'm not wrong, there are 2 components of acceleration:
One that moves the object towards the equilibrium state mostly horizontally and one vertically.
The normal component is vertical one, the tangential is horizontal.

G_t = ma_t
Gsin α = ma_t
sin 15 degrees = 0.26
a_t = 2,6 (m/s²)
G = mg = 1;
G_t = 0,26 (N) (=ma_t)
G_N = 0,74 (N)

T-G_N = ma_N
T - 0,74 = 0,1a_N

Any tips on how to get T or normal component of acceleration?

 

[scottdave]

When I'm stuck, I sometimes like to look at extreme cases, because they are simpler. Think for a moment when it is vertical. Can the string provide any force left or right? Would that be easy to find the tension at that point? Now as it swings, how do the (up/down) and (left/right) tension forces change with angle? If it helps, imagine if the string were to go horizontal what would be the forces?

 

[haruspex]

there are 2 components of acceleration:

There is one acceleration. You can resolve that into components in different directions if it helps, but that is a choice. There is no fundamental sense in which there are two components.

The normal component is vertical one, the tangential is horizontal.

How are you defining normal here? If you mean normal to the trajectory then no, that is not vertical, and the tangential is not horizontal.