Ball-Wall collision problem

[PhysicsIsKillingMe]

Problem goes: A rubber ball, traveling in a horizontal direction, strikes a vertical wall. It rebounds at right angles to the wall. The graph below illustrates the variation of the ball’s momentum p with time t when the ball is in contact with the wall.

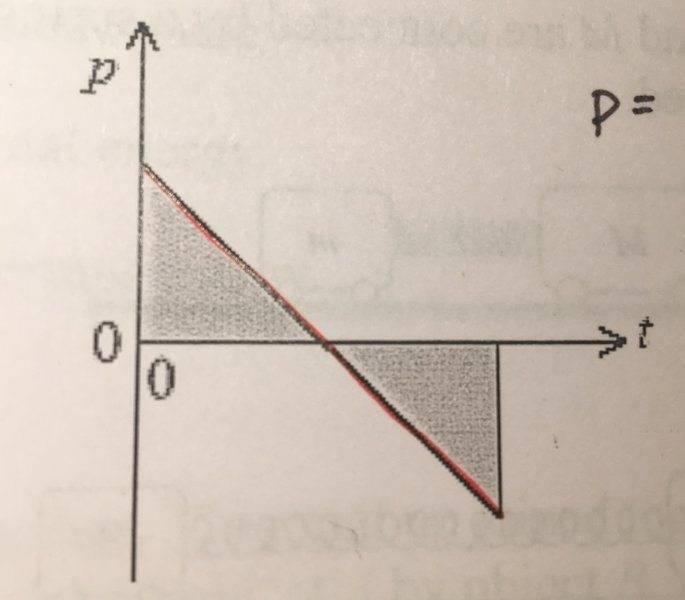
Which of the following statements is true?

A) The shaded area is equal to the force exerted by the wall on the ball.
B) The shaded area is equal to the force exerted by the ball on the wall.
C) The gradient is equal to the force exerted by the wall on the ball.
D) The gradient is equal to the force exerted by the ball on the wall.

The right answer is C. I understand how the gradient in any momentum vs time graph is the force, but I don’t understand why it’s by the wall on the ball instead of the ball on the wall.

 

[stockzahn]

Is the ball's momentum positive or negative, when touching the wall at the first time (at $t=0$ in the graph)?

 

[mjc123]

The gradient is negative, i.e. away from the wall (the ball's initial momentum is positive, i.e. towards the wall). If it was ball on wall, the gradient would be the same but with opposite sign, i.e. positive. More generally, the force acting on on an object is equal to the rate of change of momentum of the object. So in any graph like that (momentum of an object vs. time), the gradient of the line is the force acting on the object.

 

[Orodruin]

The most straightforward reasoning is to go to Newton's second law, dp/dt = F, where F by definition is the force on the body. Hence, the derivative of the momentum of the ball is equal to the total force acting on the ball, which in this case is provided by the wall.