chem_
- 1
- 0
Consider the following scenario. A material has the E-k band scheme as shown in the figure (extended scheme of zones). Could anyone give me a suggestion regarding the following :
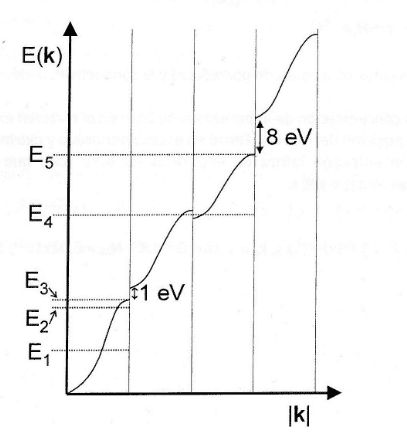
For the first case (Fermi level is the dotted line that appears for E1), I have reasoned as follows:
Would it be so?
- Electrical character of the material with the temperature.
- Sign of the Hall coefficient.
- Sign of the effective mass.
For the first case (Fermi level is the dotted line that appears for E1), I have reasoned as follows:
- As the conduction band is half-full for the Fermi level, we are dealing with a conductive material.
- The effective mass is a tensor that describes the influence of internal forces on an electron that is subjected to an external force (usually an electric field). The effective mass is inversely proportional to the curvature of the electronic band, so the effective mass is negative.
- As the effective mass is negative, the Hall's coefficient is positive.
Would it be so?