- #1
Fabrice23
- 3
- 0
How can I show that a first-degree Besselfunction a la Jn=Bessel(n,eta) for large etas always lead to something like a bathtub?
I.e. how can I show that J(n=eta) produces sth like a overshoot?
I would really appreciate every idea.
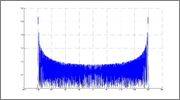
I.e. how can I show that J(n=eta) produces sth like a overshoot?
I would really appreciate every idea.
