Bending of a telescopic crane boom

[FEAnalyst]

TL;DR

How to analyze the telescopic boom of a workshop crane in terms of bending?

Hi,

how can one analyze the telescopic boom of a workshop crane in terms of bending ? Of course the worst case is when the boom is fully extended. Should we treat it as a beam with sudden change of cross-section (or otherwise - with sudden change of flexural stiffness) ? I know that there are different formulas for the deflection of such beam. Where can I find them (or how can I derive them) ? What about the stresses (are they calculated differently too) ?

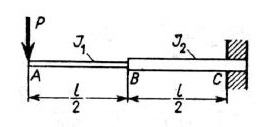
Thanks in advance for your help

 

[jrmichler]

Analyze it as two cantilever beams connected at the point where they change dimensions ($l/2$). The first beam, from C to B, has a moment curve from which you calculate vertical deflection and angular deflection at Point B. The second beam, from B to A, has those vertical and angular deflections as its boundary conditions at Point B.

Another way to look at it is the deflection, both vertical and angular, of beam B - A is added to the deflection of beam C - B.

Stress is calculated from the bending moment at a point and the section properties at that point. The plot of stress vs location will have a step change at point B.

 

[FEAnalyst]

Thanks for reply. Actually, I forgot to add that the image attached to my post is an example of a beam with sudden change of cross-section. In my case the beam will look differently. It represents a crane boom so it will be more like a simply-supported beam with overhang:

The right support is where hydraulic actuator connects with the boom.

Is it even possible to analyze such beam analytically ?

 

[Lnewqban]

It may also be important to consider the concentrated loads on the area of overlap of both sections.
In many cases the sliding is facilitated by rollers or sliding pads.
If sliding without those, the top and bottom overlapping surfaces still do not have a uniformly distribuited load or contact, due to normal clearance between both cross sections.

 

[jrmichler]

The two beams in the telescoping boom are analyzed separately.

Generally, the small telescoping beam is supported at two points, and loaded at one point. The forces at those two support points are calculated using sum of moments for the first support point, and either sum of moments or sum of forces for the second support point.

The the larger beam is loaded at two points with known forces (from above), and supported at two points. The forces at those two support points are calculated using sum of moments as above.

Now you know all forces, so you can construct moment diagrams for each of the two beams. The stresses are calculated from the moment diagrams and section properties.