Bernoulli vs conservation of momentum (Reynolds transport theorem form)

[Urmi Roy]

So I've found several instances in which Bernoulli and Conservation of momentum (in Reynolds transport theorem form) give different answers for the study of an inviscid fluid.

Let's consider a simple situation as described in my diagram attached.
Basically a tap/faucet is releasing fluid, which is known to be inviscid. We want to find the velocity at the bottom just before it hits the ground.

My solution does it out with both Bernoulli and conservation of momentum, but the factor of 2 that comes from the kinetic energy in Bernoulli doesn't appear in the final expression from

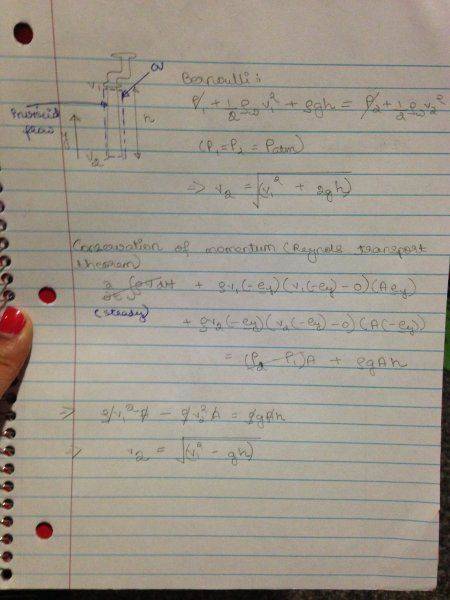conservation of momentum.

This is only a simple example and I've come across this discrepancy about the '2' several times. I'm not sure what is going on here and any help would be much appreciated!

 

[Orodruin]

The area is not constant and the flow becomes narrower as it falls as an effect of the flow speeding up. Your second expression also has the wrong sign.

 

[Urmi Roy]

Sorry about the sign problem, that's just careless of me. So apart from that, conservation of momentum doesn't give the right answer because it can't account for the area change? Does that mean that if there is an inviscid flow, it's just safer to use Bernoulli?
As before, my question is that what causes the difference between these two approaches?

 

[Orodruin]

So apart from that, conservation of momentum doesn't give the right answer because it can't account for the area change? Does that mean that if there is an inviscid flow, it's just safer to use Bernoulli?

There is nothing wrong with using momentum conservation, but you have to supplement is with additional equations describing how the fluid evolves, e.g., conservation of mass. If you do it correctly, the area as a function of the height will drop out of the equations. The only thing that went wrong was that you assumed constant area (which is an assumption that broke mass conservation).

In fact, you can derive the Bernoulli equation from momentum conservation and some additional requirements.

 

[Urmi Roy]

Oh okay, I get your point. Thanks! Just to confirm with you, I had another problem where an elevator is falling through air and the Reynolds number is found to be much larger than 1,so that the flow is approximately inviscid. Again, Bernoulli and Conservation of momentum give different answers for the terminal velocity. I'm thinking this is because at the bottom surface of the elevator there is a pressure distribution while conservation of momentum assumes an average pressure all along the surface. I can show you my working for this if you prefer.
But from your response I get that if for an inviscid flow the two approaches don't give the same answer, there's probably a mistake somewhere- they should always be equivalent.
Thanks!

 

[Orodruin]

I'm thinking this is because at the bottom surface of the elevator there is a pressure distribution while conservation of momentum assumes an average pressure all along the surface.

This is again an assumption that you might make in momentum conservation, but your assumption may or may not be justified. The momentum conservation in itself is not violated.

 

[Urmi Roy]

Thanks for all your help, Orodruin!