Bessel Equation and Bessel fuctions

[unscientific]

We first express Bessel's Equation in Sturm-Liouville form through a substitution:

Next, we consider a series solution and replace v by m where m is an integer. We obtain a recurrence relation:

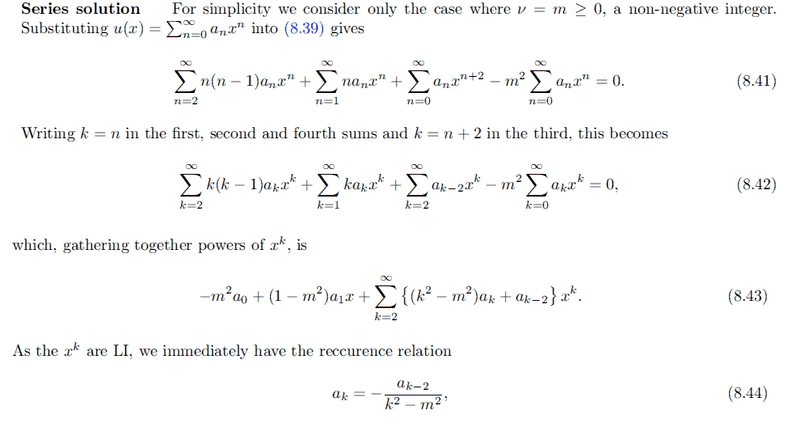
Then, since all these terms must be = 0,

Consider m = 0

First term vanishes and second term =

a₁x = 0

therefore, a₁ = 0. Then by recurrence relation above, a₁ = a₃ = a₅ = ... = a_2n-1 = 0

Then only the even series give non-zero coefficients, so we start with a₀ ≠ 0.

Consider m = 1

Second term vanishes, and first term =

a₀ = 0

By recurrence relation, this implies a_2n = 0

So we start the series with a₁ ≠ 0

Book's Explanation

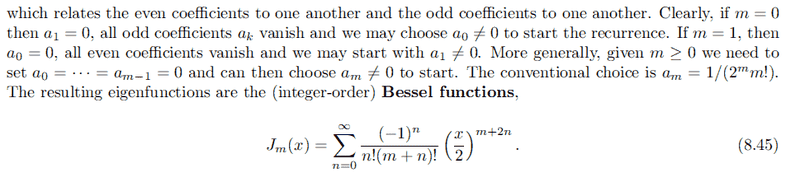
I don't understand why a₀ = a₁ = ... = a_m-1 = 0

Surely, for any value of m that is ≠ 1 we have:

$$a_{1}x = \frac{m^2}{1 - m^2} a_0$$

This doesn't imply anything above? Also, how did they get the resulting Bessel functions? It looks wildly different from mine.

a₀ = a₁ = ... = a_m-1 = 0,

$$u = \sum_{n=m}^\infty a_{n} x^n = \frac {1}{2^n n!} x^n$$

 

[AlephZero]

From 8.44 you have $(k^2 - m^2)a_k = -a_{k-2}$

When $k = m$, that is $0a_k = a_{k-2}$.

Using $a_{k-2} = 0$ and the recurrence relation, $a_{k-4} = a_{k-6} = \dots = 0$.

 

[pasmith]

Start from
$$-m^2 a_0 + (1 - m^2)a_1 x + \sum_{k= 2}^{\infty} ((k^2 - m^2)a_k + a_{k-2})x^k = 0$$

We need this equation to hold for all $x$. Thus looking at the constant term we must have
$$m^2 a_0 = 0$$
Thus if $m \neq 0$ we must have $a_0 = 0$. On the other hand if $m = 0$ then $m^2 a_0 = 0$ whatever the value of $a_0$.

Looking at the coefficient of $x^1$ we have
$$(1 - m^2)a_1 = 0$$
so that if $m \neq 1$ we are forced to take $a_1 = 0$. If $m = 1$ then $(1 - m^2)a_1 = 0$ whatever the value of $a_1$.

At order $x^2$ and higher we find that
$$(k^2 - m^2)a_k + a_{k-2} = 0$$
from which it follows that if $a_{k-2} = 0$ then we must have $a_k = 0$ unless $k = m$, in which case we can choose $a_m$ as we see fit. But this only happens if $m \geq 2$, so that $m \neq 0$ and $m \neq 1$, and by the above we must take $a_0 = a_1 = 0$. The recurrence relation then tells us that $a_0 = a_1 = \dots = a_{m - 1} = 0$.

We also have
$$((m + 1)^2 - m^2)a_{m + 1} + a_{m - 1}<br /> = (2m + 1)a_{m+1} + 0 = 0$$
so that $a_k = 0$ for $k = m + 2n + 1$, $n \geq 0$.

If $k = m + 2n$, $n \geq 0$, then
$$((m + 2n)^2 - m^2)a_{m + 2n} + a_{m + 2(n-1)} = 0$$
so that
$$a_{m + 2n} = - \frac{a_{m + 2(n-1)}}{(m^2 + 4mn + 4n^2) - m^2} <br /> = - \frac{a_{m + 2(n-1)}}{4n(m + n)}$$
which can be solved to obtain
$$a_{m + 2n} = \frac{(-1)^n}{4^n n!(m + 1) \times \dots \times (m + n) }a_m = \frac{(-1)^n m!}{2^{2n} n!(m + n)!}a_m$$
(looking at $a_{m + 2}$, $a_{m + 4}$, and $a_{m + 6}$ establishes the pattern which can then be proven by induction on $n$) from which the given series for $J_m(x)$ follows.