bobby2k
- 126
- 2
bivariate normal distribution-"converse question"
Hello, I have a theoretical question on how to use the bivariate normal distribution. First I will define what I need, then I will ask my question.
pics from: http://mathworld.wolfram.com/BivariateNormalDistribution.html
We define the bivariate normal distribution, (1):
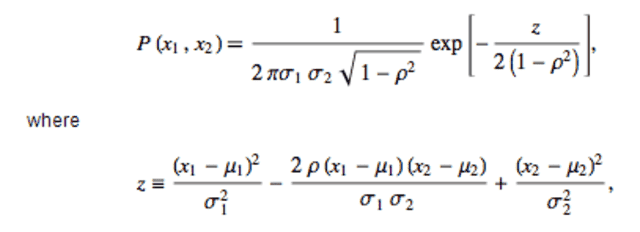
From this we get the marginal distributions:
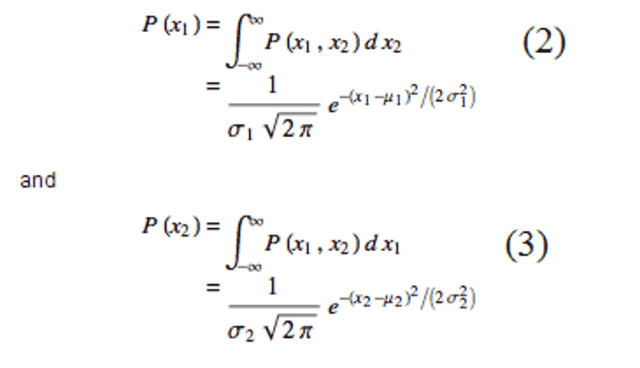
No comes my question:
Let's say that we have 2 random variables x1 and x2, and we know that each marginal distribution satisfies (2) and(3), that is, we know they are normal, and we know their mean, and variance. Suppose we also know their correlation-coefficient p. How can we now say that equation (1) is the joint probability density function. I mean, we defined it one way, and got the marginals, what is the justification that if we have 2 marginals and their p, we can go back? I mean, it is not allways true that the converse is true, why can we assume the converse here?
They used this technique in my book when proving that \bar{X} and S^{2} are independent.
Hello, I have a theoretical question on how to use the bivariate normal distribution. First I will define what I need, then I will ask my question.
pics from: http://mathworld.wolfram.com/BivariateNormalDistribution.html
We define the bivariate normal distribution, (1):
From this we get the marginal distributions:
No comes my question:
Let's say that we have 2 random variables x1 and x2, and we know that each marginal distribution satisfies (2) and(3), that is, we know they are normal, and we know their mean, and variance. Suppose we also know their correlation-coefficient p. How can we now say that equation (1) is the joint probability density function. I mean, we defined it one way, and got the marginals, what is the justification that if we have 2 marginals and their p, we can go back? I mean, it is not allways true that the converse is true, why can we assume the converse here?
They used this technique in my book when proving that \bar{X} and S^{2} are independent.
Last edited: