garthenar
- 35
- 8
- Homework Statement
- Not a specific hwk problem, but I keep getting stuck at a certain point in my Boolean simplifications. I'm hoping someone can help me figure out what steps/rules I need to apply to further simplify my Boolean expressions.
- Relevant Equations
- The basic rules/laws/theorems of Boolean Algebra
I'm suspecting consensus theorem in particular.
I was asked to use De Morgans law to find the complement of a particular equation, I applied the law correctly and simplified my solution down to
A'B'CD'+CA+CB'+D'A+D'B'
I ran the problem through a boolean simplifier to check my work. (http://tma.main.jp/logic/logic.php?lang=en&type=eq&eq=~((A+++~(~BC~D))+(~AB+++~CD)+)) and it gave me
CA+CB'+D'A+D'B'
I can't figure out how they got rid of the A'B'CD' term (is that called a term or something else?)
I have run into this situation multiple times and I just can't figure out how to get rid of the larger term (A'B'CD' term in this case). I'm sure it's simple but sometimes you just need a push in the right direction. I suspect it takes multiple steps of manipulation to pull off and that I'm just not seeing how to do that.
I've attached my work so far
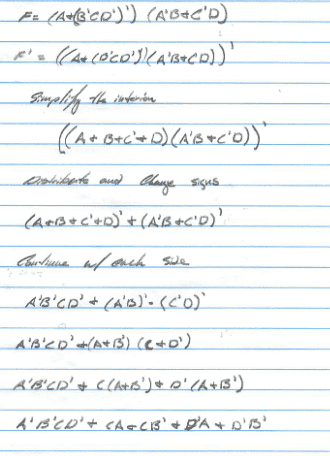
A'B'CD'+CA+CB'+D'A+D'B'
I ran the problem through a boolean simplifier to check my work. (http://tma.main.jp/logic/logic.php?lang=en&type=eq&eq=~((A+++~(~BC~D))+(~AB+++~CD)+)) and it gave me
CA+CB'+D'A+D'B'
I can't figure out how they got rid of the A'B'CD' term (is that called a term or something else?)
I have run into this situation multiple times and I just can't figure out how to get rid of the larger term (A'B'CD' term in this case). I'm sure it's simple but sometimes you just need a push in the right direction. I suspect it takes multiple steps of manipulation to pull off and that I'm just not seeing how to do that.
I've attached my work so far