What is the role of Thales' Theorem in the proof of Brahmagupta's Theorem?

[aheight]

TL;DR

Problems following proof of Bragmagupta's Theorem

Brahmagupta's theorem:

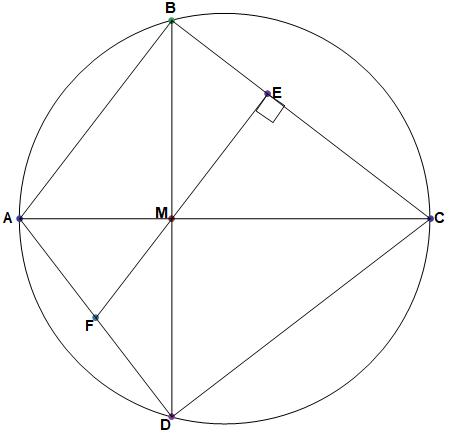
A cyclic quadrilateral is orthodiagonal (diagonals are perpendicular) if and only if the perpendicular to a side from the point of intersection of the diagonals bisects the opposite side.

But I don't understand the first step of the proof for the necessary condition from Proof Wiki: Proof of Brahmagupta's Theorem, that is, if the perpendicular bisects the opposite side then the quad is orthodiagonal. It states:

From Thales' Theorem (indirectly) we have that $AF=FM=FD$

I've looked at Thale's theorem but do not understand how we can initially state that $AF=FM=FD$ and I was wondering if someone could help me with this?

Thanks guys.

 

[mfb]

A cyclic quadrilateral is orthodiagonal (diagonals are perpendicular) if and only if the perpendicular to a side from the point of intersection of the diagonals bisects the opposite side.

That is not the same as the theorem you linked to. Proofwiki only deals with orthodiagonal quadriliterals. In that case the triangle AMD has a right angle at M, which means the angles FAM and FMA are the same, the triangle AFM is an equilateral triangle and AF=FM. AF=FD was given already.

 

[aheight]

Ok thanks MFB. I understand it now and now see why the reference to Thales was made: if $\angle AMD$ is a right angle, then we can inscribe $\triangle AMD$ in a circle with diameter AD and therefore, AM=FM since F is the midpoint.