SUMMARY
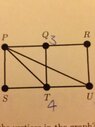
This discussion focuses on constructing breadth-first and depth-first spanning trees using a graph traversal algorithm. The breadth-first spanning tree utilizes a queue (FIFO) starting from vertex P, adding connected vertices in alphabetical order, while the depth-first spanning tree employs a stack (LIFO) for the same purpose. The final results for the breadth-first tree are confirmed to be QSTUR, aligning with the expected output from the algorithm. Both methods emphasize the importance of maintaining the correct order of vertex connections based on alphabetical precedence.
PREREQUISITES
- Understanding of graph theory concepts, specifically spanning trees
- Familiarity with queue and stack data structures
- Knowledge of breadth-first search (BFS) and depth-first search (DFS) algorithms
- Basic programming skills to implement the algorithms
NEXT STEPS
- Implement breadth-first search (BFS) in Python using the queue module
- Implement depth-first search (DFS) in Python using the stack data structure
- Explore variations of spanning tree algorithms, such as Prim's and Kruskal's algorithms
- Study graph traversal complexities and their applications in real-world scenarios
USEFUL FOR
Students, computer science enthusiasts, and software developers interested in graph algorithms and data structure optimization will benefit from this discussion.