Buoyancy and Spring force problem.

[PandaherO]

Homework Statement

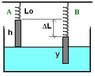
A spring with spring constant 35N/m is attached to the ceiling, and a radius=0.025m, 1.0kg metal cylinder is attached to the lower end. The cylinder is held so that the spring is neither stretched nor compressed, then a tank of water is placed under-neath with the surface of the water just touching the bottom of the cylinder. When released, the cylinder will oscillate a few times but, damped by water, reach an equilibrium position. When in equilibrium, what length of the cylinder is submerged?

Homework Equations

Fspring=-kx
Vcylinder=∏r^2h
Fb=rho*Vfluid*g

THe answer is given, (18.1cm) but I'm kinda confused as to how the solution came about

The Attempt at a Solution

Fnet=Fb-(Fg+Fspring)

rho*Vfluid*g =mg+ kx ?

Help/hints much appreciated!

 

[ehild]

Make a drawing, and find the correct direction of forces. How is the submerged length of the cylinder related to the change of length of the spring? What is V(fluid) in terms of the submerged length and radius of the cylinder? Note that you wrote the volume of a sphere as relevant equation instead of the volume of a cylinder.

ehild

 

[PandaherO]

Make a drawing, and find the correct direction of forces. How is the submerged length of the cylinder related to the change of length of the spring? What is V(fluid) in terms of the submerged length and radius of the cylinder? Note that you wrote the volume of a sphere as relevant equation instead of the volume of a cylinder.

ehild

Woops my bad, okay, I changed it to volume of a cylinder.

So in equilibrium net force is 0, and the forces in the system are Fb, Fspring, Fg
After drawing,
Fnet=(Fb+Fspring)-Fg
Fb+Fspring=Fg

Fb=rho of water* Vfluid displaced, which would be broken down into ∏r^2 *h that's height of the object, or cylinder? *g

so Fb=rho*Vf (or ∏r^2h)*g
Fg=just the cylinder's weight = 1kg(9.8)
Fspring=(35N/m)(x)

generally h submerged is= h of object- h object above water level

So when you mentioned, that the submerged length of the cylinder is related to the change of length of the spring, do you mean the submerged length of the cylinder would factor into
the equation Area*(Hobj-change of length of spring) above for Fb?

 

[ehild]

So when you mentioned, that the submerged length of the cylinder is related to the change of length of the spring, do you mean the submerged length of the cylinder would factor into
the equation Area*(Hobj-change of length of spring) above for Fb?

I do not understand. Could you draw a picture? Or look at my one and say how is the submerged length (y) related to the change of the length of the spring(ΔL). How much water is displaced in terms of y?

ehild

 

[Jehosiphat]

You have to make a substitution. Usually the questions that say "and then" somewhere require a comparison of before and after. So first find the length of the spring at equilibrium Fg=-kx. 1.0*9.8=-35x. x=.28m. Then note that the tub of water will add a buoyant force Fb, such that the spring will relax a little, and compress. So delta L= .28-x. You don't know the height of the cylinder, but the height of the 'cylinder of water' that is displaced is also going to equal .28-x. So you should end up with:

Fb+kx= Fg
rho fluid * Volume fluid displaced * g + 35 * x = mass obj. * g
1000 * (.025^2 * pi * (.28-x))(9.8) + 35 * (.28-x) = 1.0 * 9.8
19.24225(.28-x) + 35(.28-x)= 9.8
(5.3878 - 19.24225x) + (9.8 - 35x) = 9.8
5.3878 + 9.8 -9.8 = 54.24225x
x=5.3878/ 54.24225
x= 0.099328

delta L = .28- 0.09932
= .18067m
= 18.067 cm , 18.1 cm.

 

[PandaherO]

oh, I was using just 0.28 before, I see now.
Thanks! :) (especially ehild for drawing the diagram)