cy19861126
- 69
- 0
Homework Statement
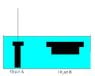
Two objects of the same mass and volume but different shape are suspended from strings in a tank of water as shown. Is there more tension force on the string by object A or B? Link to the picture can be found at http://students.washington.edu/cy1126/Buoyancy.JPG
Homework Equations
P = pgh, where p = density
F = PA
P = pghA
B = pgh1A1 - pgh2A2
The Attempt at a Solution
I think that object A is more buoyant than object B because object A has a greater difference of depth than object B therefore contributing to a greater buoyancy. For object B, although the force on top of it is greater due to larger area, the "difference" of area is almost the same as object A. I am not sure about my reasoning here. Can someone check my answer for me as well as giving me some clue if I am getting the wrong concept
Attachments
Last edited by a moderator: