Vinita
- 23
- 0
Homework Statement
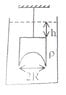
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is?
Homework Equations
Force = Pressure x Area
The Attempt at a Solution
Since the object is in equilibrium, I balanced the 3 forces acting on it.
Weight of the body = Force on the top of the cylinder - Force on the bottom of the cylinder
⇒Mg = ρgh(πR²) - F (ignoring atmospheric pressure)
⇒F = πR²hρg - Mg
But the answer is F = ρg( V + πR²h)
What did I do wrong?