Calaculate a Ln without calculator

[baby_1]

Hello
Im solving a problem with calculator to find the zeta in this equation

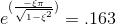
but as i see some persons they solved this equation with different numbers(1.63 ) without calculator.now i want to know
how can fine zeta in this equation without calculator and fast?

 

[mfb]

ln(.163) = -2 + ln(e^2*0.163) ≈ -2 + ln(7*0.163) ≈ -2 + ln(1.1) ≈ -2 + 0.1 = -1.9
$-z\pi \approx -1.9 \sqrt{1-z^2}$
=> z>0
$z^2 \pi^2 \approx 3.6 - 3.6 z^2$
$z^2 (10+3.6) \approx 3.6$
$z^2 \approx \frac{3.6}{13.8} \approx \frac{4}{15} \approx \frac{2.7}{10} = 0.27$
$z \approx 0.5$
Solving speed ≈ typing speed
That is very close to the exact value and indicates that the .163 and the formula have some special meaning.

Edit: Fixed small error.