LearninDaMath
- 295
- 0
My math calc 1 class starts just 10 minutes after my physics class ends and it's on the opposite side of campus and yesterday I had my first exam in physics and ended up missing the first 3 minutes of my math class lecture. I copied the notes from the board, but didn't hear what he was saying about the graph. He's an excellent professor, but without hearing what he was saying, I can't figure out what the notes are talking about.
Can anyone look at this graph and the formula and decipher what concept/lesson the professor was describing?
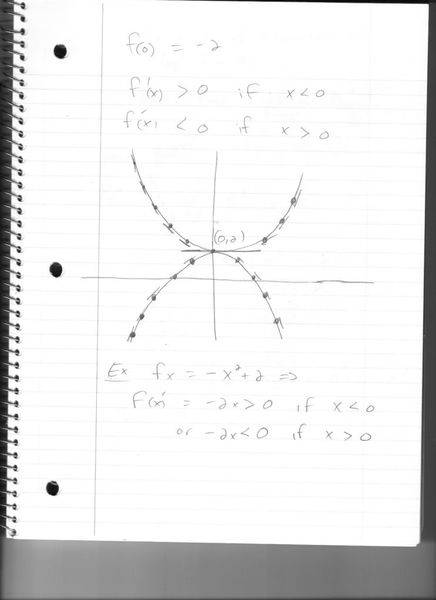
perhaps f(0) = -2 doesn't correspond to anything on this graph..it could be from somthing else he had already erased before I got to class, i just don't know.
So I'm trying to figure out what it all means.
Can anyone look at this graph and the formula and decipher what concept/lesson the professor was describing?
perhaps f(0) = -2 doesn't correspond to anything on this graph..it could be from somthing else he had already erased before I got to class, i just don't know.
So I'm trying to figure out what it all means.