DuckAmuck
- 238
- 40
- TL;DR
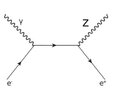
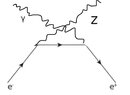
- Process of electron and positron annihilation to photon and Z boson
Looking to calculate the amplitude and cross section of the process: electron + positron to photon + Z boson.
Basically the annihilation resulting in Z + gamma rather than gamma +gamma.
My question is mainly about how to deal with the polarization states with the Z boson, since there are 3 and how to handle to the Lorentz gauge wrt to the Z field. Any help will be appreciated.
Basically the annihilation resulting in Z + gamma rather than gamma +gamma.
My question is mainly about how to deal with the polarization states with the Z boson, since there are 3 and how to handle to the Lorentz gauge wrt to the Z field. Any help will be appreciated.