Understanding the (polarized) cross section for Compton Scattering by electrons

[JD_PM]

TL;DR Summary

I am studying the derivation of the polarized cross-section for Compton Scattering by electrons (i.e. both initial and final electron and photon states are set) from Mandl & Shaw (M&S)'s QFT book (chapter 8, section 8.6) and vanhees71's Manuscript (6.5.1 Compton Scattering).

I have specific questions, but let's first give context.

Initially we have an electron with momentum $p=(E, \vec p)$ and spin state $u_r (\vec p)$ and a photon with momentum $k=(\omega, \vec k)$ and polarization state $\epsilon_s (\vec k)$.
Finally we have $p'=(E', \vec p')$, $u_r' (\vec p')$, $k'=(\omega', \vec k')$, $\epsilon_s' (\vec k')$

I understand that the differential-cross section for Compton Scattering by electrons is given by (more details here):

$$\frac{d \sigma}{d \Omega} = \frac{m^2 \omega'}{16 \pi^2 E E' \omega v_{rel}} \Big[ \Big( \frac{\partial(E'+\omega')}{\partial \omega'}\Big)_{\theta \phi} \Big]^{-1} |\mathscr{M}|^2 \ \ \ \ (1)$$

Where $(\theta, \phi)$ are the polar angles of $\vec k'$ and $d \Omega = \sin \theta d \theta d \phi$ is the corresponding infinitesimal solid angle. We take $\vec k$ as the polar coordinate axis, so that $\vec k \cdot \vec k' = \omega \omega' \cos \theta$ (where $\cos \theta$ arises due to the definition of the dot product).

Conservation of momentum gives

$$p+k=p'+k' \ \ \ \ (2)$$

The Feynman Amplitudes associated to these two figures are as follows

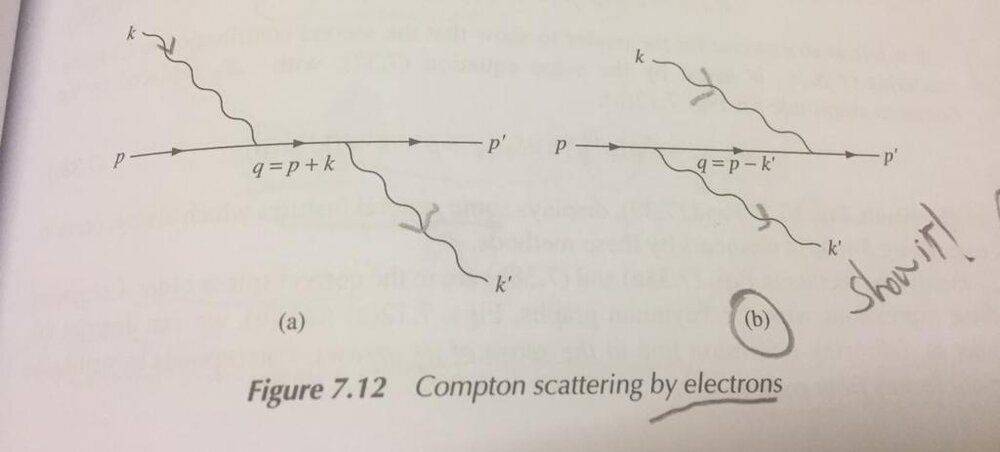$$\mathscr{M}=\mathscr{M}_a+\mathscr{M}_b \ \ \ \ (3)$$

$$\mathscr{M}_a = -i e^2 \frac{\bar u' \gamma^{\mu} \epsilon_{\mu}' (\gamma^{\mu} f_{\mu}+m) \gamma^{\mu} \epsilon_{\mu} u}{2(pk)}, \ \ \ \ \mathscr{M}_b = i e^2 \frac{\bar u' \gamma^{\mu} \epsilon_{\mu}' (\gamma^{\mu} g_{\mu}+m) \gamma^{\mu} \epsilon_{\mu}' u}{2(pk')} \ \ \ \ (4)$$

Where

$$f:=p+k, \ \ \ \ g:=p-k'$$

Eq. (3) is manifestly covariant and must be equivalent (I did not check it out myself though) to vanhees71's equation (6.128).

Experimentally the photon beam (usually) aims at a target of nearly stationary electrons. We now move to the LAB frame, which means that we have

$$p=(m, 0, 0, 0), \ \ \ \ \vec p' = \vec k - \vec k' \ \ \ \ (5)$$

Thus the energy-momentum equation yields

$$E' = \Big( m^2 + (\vec k - \vec k')^2 \Big)^{1/2} = \Big( m^2 + \omega^2 + \omega'^2 - 2\omega\omega' \cos\theta \Big)^{1/2} \ \ \ \ (6)$$

Mandl & Shaw asserted that from equation (2) we can get

$$pk=p'k+k'k=pk'+k'k \ \ \ \ (7)$$

And that Eq. (7) reduces to

$$\omega' = \frac{m \omega}{m+\omega(1-\cos\theta)} \ \ \ \ (8)$$

From Eq. (6) we get

$$\Big( \frac{\partial(E'+\omega')}{\partial \omega'}\Big)_{\theta \phi} = \frac{m \omega}{E' \omega'} \ \ \ \ (9)$$

Then, plugging back into (1) we get the differential cross section in the LAB frame

$$\Big( \frac{d \sigma}{d \Omega}\Big)_{LAB} = \frac{1}{(4 \pi)^2} \Big( \frac{\omega'}{\omega}\Big)^2 |\mathscr{M}|^2 \ \ \ \ (10)$$

These are my questions:

1) Where's Eq. (7) coming from?

M&S stated it comes from equation (2). However, I solve for $p$ and multiply (on the right) by $k$ but don't get (7)

$$pk = p'k+k'k-kk \neq p'k+k'k$$

$$pk = p'k+k'k-kk \neq pk'+k'k$$

2) Where's Eq. (8) coming from?

Let's assume Eq. (7); thus we have (recalling the definition of the 4 inner product $p_1 \cdot p_2 = E_1 E_2 - \vec p_1 \cdot \vec p_2$)

$$(m\omega, 0)=(m \omega + \omega' \omega, -(\vec k - \vec k') \cdot \vec k - \vec k' \cdot \vec k)=(m \omega' + \omega' \omega, \vec k' \cdot \vec k)$$

Simplifying a bit we get

$$(m\omega, 0)=(m \omega + \omega' \omega, -\vec k \cdot \vec k )=(m \omega' + \omega' \omega, \vec k' \cdot \vec k)$$

Recalling that $\vec k \cdot \vec k' = \omega \omega' \cos \theta$ we get

$$(m\omega, 0)=(m \omega + \omega' \omega, -\omega^2 \cos \theta )=(m \omega' + \omega' \omega, \omega' \omega \cos \theta)$$

So we end up with these two equations

$$m\omega=m\omega+\omega'\omega=m\omega'+\omega'\omega \ \ \ \ (*)$$

$$\omega' \cos \theta=-\omega \cos \theta \ \ \ \ (**)$$

Mmm Eq. (*) is trivial so it tells us nothing interesting, but what can we say about $(\omega'+\omega)\cos\theta=0$? Does it lead to Eq. (8)?

3) I am not getting Eq. 9

It has to be simply about taking the partial derivative but I am making a mistake I do not see...

$$\frac{\partial}{\partial \omega'} (E'+\omega') = \frac{\partial}{\partial \omega'} \Big[ \Big( m^2 + \omega^2 + \omega'^2 - 2\omega\omega' \cos\theta \Big)^{1/2}+\omega' \Big] = \frac{\omega'-\omega \cos \theta}{\sqrt{m^2 + \omega^2 + \omega'^2 - 2\omega\omega' \cos\theta}}+1=\frac{\omega'-\omega \cos \theta+E}{E} \neq \frac{m \omega}{E' \omega'}$$

Any help is appreciated.

Thank you

 

[Dr.AbeNikIanEdL]

For the first two:

1) $k$ should be an on-shell photon momentum, so $k^2=0=(k^\prime)^2$. Similarly $p^2=m^2=(p^\prime)^2$. From energy-momentum conservation (2) it then also follows that $p^\prime k = pk^\prime$.

2) Why do you have vector equations there? Some of them look definitely wrong as they imply things like $\vec{k}\vec{k}=0$, but I don't understand where they come from anyway. Eq. (7) is a relation between the scalars $p\cdot k$, $p\cdot k^\prime$ and $k\cdot k^\prime$. Calculating each of them in the rest frame of the initial electron, i.e. where $p=(m,\vec{0})$, $k=(\omega,\vec{k})$, $k^\prime=(\omega^\prime,\vec{k}^\prime)$ and using $\vec{k}\vec{k}^\prime=\omega\omega^\prime \cos\theta$ should almost immediately give (8) from the second version of (7).

 

[JD_PM]

For the first two:

1) $k$ should be an on-shell photon momentum, so $k^2=0=(k^\prime)^2$. Similarly $p^2=m^2=(p^\prime)^2$. From energy-momentum conservation (2) it then also follows that $p^\prime k = pk^\prime$.

Oh I see so we take Eq. (2), solve it for $p$ and multiply it (on the right side) by $k$

$$p \cdot k = p' \cdot k + k' \cdot k - k \cdot k$$

Due to the on-shell condition $k^2=0=(k^\prime)^2$, $k \cdot k=0$. Thus I get the first equality on Eq. (7)

$$p \cdot k = p' \cdot k + k' \cdot k$$

I still have to proof the second equality on Eq. (7).

$$p \cdot k = p \cdot k' + k' \cdot k$$

This is my reasoning:

We now solve Eq. (2) for $p'$, multiply (on the right side) by $k'$

$$p' \cdot k' = p \cdot k' + k \cdot k' - k' \cdot k'$$

Due to the on-shell condition $k^2=0=(k^\prime)^2$, $k' \cdot k'=0$. Thus I get

$$p' \cdot k' = p \cdot k' + k \cdot k'$$

Mmm but I am not really convinced because to show Eq. (7) I need $p' \cdot k'=p \cdot k$ to hold and I think this is not true...

.2) Why do you have vector equations there? Some of them look definitely wrong as they imply things like $\vec{k}\vec{k}=0$, but I don't understand where they come from anyway. Eq. (7) is a relation between the scalars $p\cdot k$, $p\cdot k^\prime$ and $k\cdot k^\prime$. Calculating each of them in the rest frame of the initial electron, i.e. where $p=(m,\vec{0})$, $k=(\omega,\vec{k})$, $k^\prime=(\omega^\prime,\vec{k}^\prime)$ and using $\vec{k}\vec{k}^\prime=\omega\omega^\prime \cos\theta$ should almost immediately give (8) from the second version of (7).

Ahhh big mistake of mine! Now I got it, thanks

Eq. (7) tells us that

$$p \cdot k = p \cdot k' + k \cdot k'$$

Where

$$p \cdot k=m\omega$$

$$p \cdot k'=m\omega'$$

$$k \cdot k'=\omega\omega'-\vec k \cdot \vec k'$$

Thus we get Eq. (8)

$$m\omega=m\omega'+\omega\omega'(1-\cos \theta)$$

$$\omega'=\frac{m\omega}{m+\omega(1-\cos \theta)}$$

 

[Dr.AbeNikIanEdL]

Mmm but I am not really convinced because to show Eq. (7) I need p′⋅k′=p⋅kp′⋅k′=p⋅kp' \cdot k'=p \cdot k to hold and I think this is not true...

Try squaring both sides of (2)...

Spoiler

Or first subtract $k$ and $k^\prime$ from both sides and then square to immediately get the second expression of (7) from the first.

 

[JD_PM]

Alright so indeed we have $p' \cdot k'=p \cdot k$, thank you.

About 3). There has to be a naive mistake, if I find it I'll post it.