chwala
Gold Member
- 2,827
- 415
- Homework Statement
- See attached
- Relevant Equations
- Deductive Geometry- Alternate segment theorem
Question;
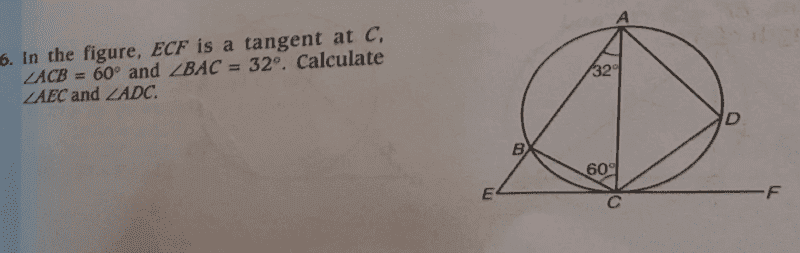
Text Solution;
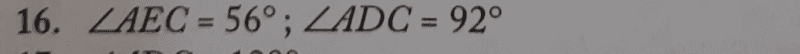
My reasoning;
##∠ABC= 180^0 -(32^0+60^0)##
=##88^0##
##∠ABC=∠ACF=88^0## (Alternate segment theorem).
##∠EBC=92^0## i.e angles lying on a straight line and ##∠BCE=180^0 -(88^0+60^0)=32^0## therefore;
##∠BEC=180^0 -(32^0+92^0)=56^0##
##∠ECA=∠ADC=32^0+60^0=92^0## (by Alternate segment theorem).
Cheers...there may be another way of looking at this...
Text Solution;
My reasoning;
##∠ABC= 180^0 -(32^0+60^0)##
=##88^0##
##∠ABC=∠ACF=88^0## (Alternate segment theorem).
##∠EBC=92^0## i.e angles lying on a straight line and ##∠BCE=180^0 -(88^0+60^0)=32^0## therefore;
##∠BEC=180^0 -(32^0+92^0)=56^0##
##∠ECA=∠ADC=32^0+60^0=92^0## (by Alternate segment theorem).
Cheers...there may be another way of looking at this...
