- #1
Mordred
- 2,090
- 106
Universe geometry article simpify?
article development for the Forum on geometry suggestions, as well as any errors etc are welcome
particularly on how to keep the FLRW metrics but simplify the explanation...
Universe geometry
The origins of the universe is unknown in cosmology. The hot big bang model only covers the history of the universe from 10-43 seconds forward. Prior to that is described as a singularity. However its important to note that the singularity is not a black hole style. Instead singularity in this case simply means a point in time where our mathematics can no longer accurately describe it. Numerous youtube videos and pop media articles would have you believe our universe exploded from some super particle. This was never predicted by the hot big bang model.
The observable universe which is the portion we can see is a finite, sphere with a radius of 46 Gly, which is equal to 46 billion light years. The 46 Gly particle horizon refers to the today's distance of objects, whose radiation emitted in the past we receive today. The overall size of the universe is not known, it could be infinite or finite. If its infinite now then it would be infinite in the past, a finite value can never become infinite. So why is geometry so important to cosmology if we know the size of the observable universe? The answer to that question lies in how geometry affects the following aspects, Light paths, rate of expansion or collapse and overall shape.
In regards to light paths and geometry a closed universe described as a sphere will have two beams of light emitted at different angles eventually converge. An open hyperbolic universe such as a saddlebag will have those same two light beams diverge. A flat universe will have parallel light paths (provided the beams at emission were parallel to begin with)
You will notice on each image there is a triangle, this triangle represents how the geometry affects our measurements. In a flat curvature the three angles of a equilateral triangle will add up to 1800. A positive curvature will add up to greater than 1800, a negative curvature will add up to less than 1800
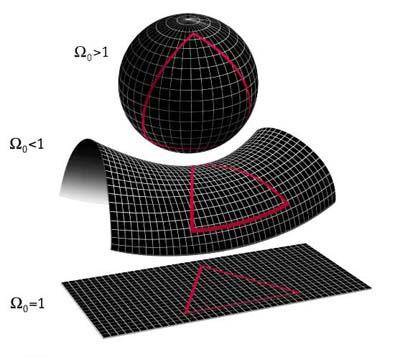
Image from http://universeadventure.org
The topography of the universe is determined by a comparison of the actual density (total density) as compared to the critical density. The critical density is represented by the following formula
[itex]\rho_{crit} = \frac{3c^2H^2}{8\pi G}[/itex]
P=pressure
c=speed of light
G= gravitational constant.
density is represented by the Greek letter Omega [itex]\Omega[/itex] so critical density is [itex]\Omega crit[/itex]
total density is
[itex]\Omega[/itex]total=[itex]\Omega[/itex]dark matter+[itex]\Omega[/itex]baryonic+[itex]\Omega[/itex]radiation+[itex]\Omega[/itex]relativistic radiation+[itex]{\Omega_ \Lambda}[/itex]
[itex]\Lambda[/itex] or Lambda is the value of the cosmological constant often referred to as "dark energy" more accurately it is the vacuum pressure that attributes to expansion.
the subscript "0"for [itex]\Omega[/itex] shown in the image above denotes time in the present.
Energy-density is the amount of energy stored per unit volume of space or region. Energy per unit volume has the same physical units as pressure, and in many circumstances is an exact synonym.
[itex]\Omega=\frac{P_{total}}{P_{crit}}[/itex]
or alternately
[itex]\Omega=\frac{\Omega_{total}}{\Omega_{crit}}[/itex]
Geometry in 2D
In developing a theory of space-time, where curvature is related to the mass-energy density, Scientists needed a way of mathematically describing curvature. Since picturing the curvature of a four-dimensional space-time is difficult to visualize. We will start by considering ways of describing the curvature of two-dimensional spaces and progress to 4 dimensional spaces.
The simplest of two-dimensional spaces is a plane, on which Euclidean geometry holds.
This is the geometry that we learned in high school: parallel lines will go off to infinity
without ever crossing; triangles have interior angles that add up to 180. Pythagoras’
theorem which relates the lengths of the sides of a right triangle also holds:
c2 = a2 + b2
where c is the length of the hypotenuse of the right triangle, and a and b are the
lengths of the other two sides. One can generalize the Pythagorean theorem to three dimensions as well:
c2= a2 + b2 + c2
see image 2.0 below
On a plane, a "geodesic" is a straight line(shortest distance between two points). If a triangle is constructed on a flat 2 dimensional plane by connecting three points with geodesics. The curvature can be represented in 2D, if you establish each angle of a equilateral triangle with
[itex]\alpha[/itex],[itex]\beta[/itex],[itex]\gamma[/itex] for a flat geometry this follows the relation
[itex]\alpha[/itex]+[itex]\beta[/itex]+[itex]\gamma[/itex]=[itex]\pi[/itex].

image 1.0
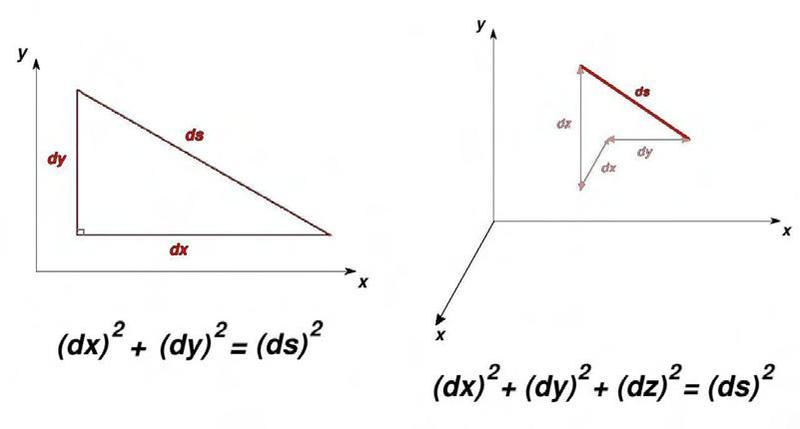
image 2.0 reference (3)
On a plane, (shown above) we can set up a cartesian coordinate system, and assign to every point a coordinate (x; y). On a plane, the distance ds between points (dx and dy) is given by the relation
[itex]d{s^2}=d{x^2}+d{y^2}[/itex]
If a triangle is constructed on the surface of the sphere by connecting the angles will obey the relation
[itex]\alpha[/itex]+[itex]\beta[/itex]+[itex]\gamma[/itex]=[itex]\pi+{AR^2}[/itex]
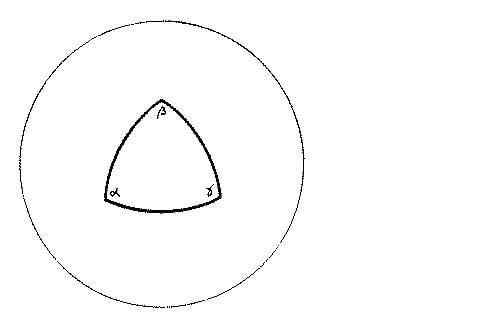
image 1.1
where A is the area of the triangle, and R is the radius of the sphere. All spaces in which
[itex]\alpha[/itex]+[itex]\beta[/itex]+[itex]\gamma[/itex]>[itex]\pi[/itex] are called positively curved" spaces. It is a space where the curvature is homogeneous and isotropic; no matter where you draw a triangle on the surface of a sphere, or how you orient it, it must always satisfy the above equation.
"On the surface of a sphere, we can set up polar coordinates "north pole" and "south pole" and by picking a geodesic from the north to south pole to be the "prime meridian". If r is the distance from the north pole, and [itex]\theta[/itex] is the azimuthal. angle measured relative to the prime meridian,"(1) then the distance ds between a point (r; [itex]\theta[/itex]) and another nearby point (r+dr+[itex]\theta[/itex]+d[itex]\theta[/itex]) is given by the relation
[itex]{ds^2} = {dr^2} + {R^2} {sin^2}(r/R)d\theta^2[/itex]
"An example of a negatively curved two-dimensional space is the hyperboloid, or saddle-shape. A surface of constant negative curvature. The saddle-shape has constant curvature only in the central region, near the "seat" of the saddle."(1) Consider a two-dimensional surface of constant negative curvature, with radius of curvature R. If a triangle is constructed on this surface by connecting three points with geodesics, the angles at its vertices [itex]\alpha[/itex]
[itex]\beta[/itex],[itex]\gamma[/itex] obey the relation [itex]\alpha[/itex]+[itex]\beta[/itex]+[itex]\gamma[/itex]=[itex]\pi-{AR^2}[/itex].
[itex]{ds^2} = {dr^2} + {R^2} {sinH^2}(r/R)d\theta^2[/itex]
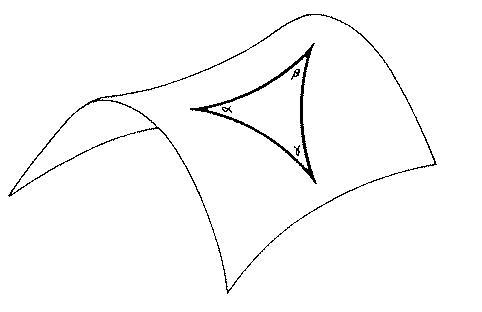
image 1.2
A negative curvature is an open topography
If a two-dimensional space has curvature or flat which is homogeneous and isotropic, its geometry can
be specified by two quantities k, and R. The number k, called the curvature constant, R is the radius
k = 0 for a flat space,
k = +1 for a positively curved space,
k = -1 for a negatively curved space
Geometry in 3D
A two dimensional space can be extended to a three-dimensional space, if its curvature is homogeneous and isotropic, must be flat, or have uniform positive curvature, or have
uniform negative curvature. If a three-dimensional space is flat (k = 0), it
has the metric
ds2 = dx2 + dy2 + dz2 ;
expressed in cartesian coordinates or
[itex]{ds^2} = {dr^2} +{r^2}[d\theta^2 + {sin^2} d\phi^2][/itex]
If a three-dimensional space has uniform positive curvature (k = +1), its
metric is
[itex]{ds^2} = {dr^2} +{R^2}{sin^2}(r/R)[d\theta^2 + {sin^2}\theta d\phi^2][/itex]
A negative curvature in the uniform portion has the metric (k=-1)
[itex]{ds^2} = {dr^2} +{R^2}{sinH^2}(r/R)[d\theta^2 + {sin^2}\theta d\phi^2][/itex]
Geometry in 4D
Thus far we have discussed the 2 and 3 dimensional components. The Friedmann-Lemaitre-Robertson-Walker metric (FLRW) can be used to describe the 4D dimensions with the use of a(t). a(t) is the scale factor. See the redshift and expansion article for more information or the cosmocalc link on the main page. Scale factor in a homogeneous and isotropic universe describes how the universe expands or contracts with time.
The FLRW metric can be written in the form
[itex]d{s^2}=-{c^2}d{t^2}+a({t^2})[d{r^2}+{S,k}{(r)^2}d\Omega^2][/itex]
references
(1)"Introductory to Cosmology" Barbera Ryden"
images 1.0,1.1 and 1.2 (see (1))
(2)"Modern Cosmology" Scott Dodelson
(3)"lecture notes, Introductory to Cosmology" Dr. Ka Chan Lu
article development for the Forum on geometry suggestions, as well as any errors etc are welcome
particularly on how to keep the FLRW metrics but simplify the explanation...
Universe geometry
The origins of the universe is unknown in cosmology. The hot big bang model only covers the history of the universe from 10-43 seconds forward. Prior to that is described as a singularity. However its important to note that the singularity is not a black hole style. Instead singularity in this case simply means a point in time where our mathematics can no longer accurately describe it. Numerous youtube videos and pop media articles would have you believe our universe exploded from some super particle. This was never predicted by the hot big bang model.
The observable universe which is the portion we can see is a finite, sphere with a radius of 46 Gly, which is equal to 46 billion light years. The 46 Gly particle horizon refers to the today's distance of objects, whose radiation emitted in the past we receive today. The overall size of the universe is not known, it could be infinite or finite. If its infinite now then it would be infinite in the past, a finite value can never become infinite. So why is geometry so important to cosmology if we know the size of the observable universe? The answer to that question lies in how geometry affects the following aspects, Light paths, rate of expansion or collapse and overall shape.
In regards to light paths and geometry a closed universe described as a sphere will have two beams of light emitted at different angles eventually converge. An open hyperbolic universe such as a saddlebag will have those same two light beams diverge. A flat universe will have parallel light paths (provided the beams at emission were parallel to begin with)
You will notice on each image there is a triangle, this triangle represents how the geometry affects our measurements. In a flat curvature the three angles of a equilateral triangle will add up to 1800. A positive curvature will add up to greater than 1800, a negative curvature will add up to less than 1800
Image from http://universeadventure.org
The topography of the universe is determined by a comparison of the actual density (total density) as compared to the critical density. The critical density is represented by the following formula
[itex]\rho_{crit} = \frac{3c^2H^2}{8\pi G}[/itex]
P=pressure
c=speed of light
G= gravitational constant.
density is represented by the Greek letter Omega [itex]\Omega[/itex] so critical density is [itex]\Omega crit[/itex]
total density is
[itex]\Omega[/itex]total=[itex]\Omega[/itex]dark matter+[itex]\Omega[/itex]baryonic+[itex]\Omega[/itex]radiation+[itex]\Omega[/itex]relativistic radiation+[itex]{\Omega_ \Lambda}[/itex]
[itex]\Lambda[/itex] or Lambda is the value of the cosmological constant often referred to as "dark energy" more accurately it is the vacuum pressure that attributes to expansion.
the subscript "0"for [itex]\Omega[/itex] shown in the image above denotes time in the present.
Energy-density is the amount of energy stored per unit volume of space or region. Energy per unit volume has the same physical units as pressure, and in many circumstances is an exact synonym.
[itex]\Omega=\frac{P_{total}}{P_{crit}}[/itex]
or alternately
[itex]\Omega=\frac{\Omega_{total}}{\Omega_{crit}}[/itex]
Geometry in 2D
In developing a theory of space-time, where curvature is related to the mass-energy density, Scientists needed a way of mathematically describing curvature. Since picturing the curvature of a four-dimensional space-time is difficult to visualize. We will start by considering ways of describing the curvature of two-dimensional spaces and progress to 4 dimensional spaces.
The simplest of two-dimensional spaces is a plane, on which Euclidean geometry holds.
This is the geometry that we learned in high school: parallel lines will go off to infinity
without ever crossing; triangles have interior angles that add up to 180. Pythagoras’
theorem which relates the lengths of the sides of a right triangle also holds:
c2 = a2 + b2
where c is the length of the hypotenuse of the right triangle, and a and b are the
lengths of the other two sides. One can generalize the Pythagorean theorem to three dimensions as well:
c2= a2 + b2 + c2
see image 2.0 below
On a plane, a "geodesic" is a straight line(shortest distance between two points). If a triangle is constructed on a flat 2 dimensional plane by connecting three points with geodesics. The curvature can be represented in 2D, if you establish each angle of a equilateral triangle with
[itex]\alpha[/itex],[itex]\beta[/itex],[itex]\gamma[/itex] for a flat geometry this follows the relation
[itex]\alpha[/itex]+[itex]\beta[/itex]+[itex]\gamma[/itex]=[itex]\pi[/itex].
image 1.0
image 2.0 reference (3)
On a plane, (shown above) we can set up a cartesian coordinate system, and assign to every point a coordinate (x; y). On a plane, the distance ds between points (dx and dy) is given by the relation
[itex]d{s^2}=d{x^2}+d{y^2}[/itex]
If a triangle is constructed on the surface of the sphere by connecting the angles will obey the relation
[itex]\alpha[/itex]+[itex]\beta[/itex]+[itex]\gamma[/itex]=[itex]\pi+{AR^2}[/itex]
image 1.1
where A is the area of the triangle, and R is the radius of the sphere. All spaces in which
[itex]\alpha[/itex]+[itex]\beta[/itex]+[itex]\gamma[/itex]>[itex]\pi[/itex] are called positively curved" spaces. It is a space where the curvature is homogeneous and isotropic; no matter where you draw a triangle on the surface of a sphere, or how you orient it, it must always satisfy the above equation.
"On the surface of a sphere, we can set up polar coordinates "north pole" and "south pole" and by picking a geodesic from the north to south pole to be the "prime meridian". If r is the distance from the north pole, and [itex]\theta[/itex] is the azimuthal. angle measured relative to the prime meridian,"(1) then the distance ds between a point (r; [itex]\theta[/itex]) and another nearby point (r+dr+[itex]\theta[/itex]+d[itex]\theta[/itex]) is given by the relation
[itex]{ds^2} = {dr^2} + {R^2} {sin^2}(r/R)d\theta^2[/itex]
"An example of a negatively curved two-dimensional space is the hyperboloid, or saddle-shape. A surface of constant negative curvature. The saddle-shape has constant curvature only in the central region, near the "seat" of the saddle."(1) Consider a two-dimensional surface of constant negative curvature, with radius of curvature R. If a triangle is constructed on this surface by connecting three points with geodesics, the angles at its vertices [itex]\alpha[/itex]
[itex]\beta[/itex],[itex]\gamma[/itex] obey the relation [itex]\alpha[/itex]+[itex]\beta[/itex]+[itex]\gamma[/itex]=[itex]\pi-{AR^2}[/itex].
[itex]{ds^2} = {dr^2} + {R^2} {sinH^2}(r/R)d\theta^2[/itex]
image 1.2
A negative curvature is an open topography
If a two-dimensional space has curvature or flat which is homogeneous and isotropic, its geometry can
be specified by two quantities k, and R. The number k, called the curvature constant, R is the radius
k = 0 for a flat space,
k = +1 for a positively curved space,
k = -1 for a negatively curved space
Geometry in 3D
A two dimensional space can be extended to a three-dimensional space, if its curvature is homogeneous and isotropic, must be flat, or have uniform positive curvature, or have
uniform negative curvature. If a three-dimensional space is flat (k = 0), it
has the metric
ds2 = dx2 + dy2 + dz2 ;
expressed in cartesian coordinates or
[itex]{ds^2} = {dr^2} +{r^2}[d\theta^2 + {sin^2} d\phi^2][/itex]
If a three-dimensional space has uniform positive curvature (k = +1), its
metric is
[itex]{ds^2} = {dr^2} +{R^2}{sin^2}(r/R)[d\theta^2 + {sin^2}\theta d\phi^2][/itex]
A negative curvature in the uniform portion has the metric (k=-1)
[itex]{ds^2} = {dr^2} +{R^2}{sinH^2}(r/R)[d\theta^2 + {sin^2}\theta d\phi^2][/itex]
Geometry in 4D
Thus far we have discussed the 2 and 3 dimensional components. The Friedmann-Lemaitre-Robertson-Walker metric (FLRW) can be used to describe the 4D dimensions with the use of a(t). a(t) is the scale factor. See the redshift and expansion article for more information or the cosmocalc link on the main page. Scale factor in a homogeneous and isotropic universe describes how the universe expands or contracts with time.
The FLRW metric can be written in the form
[itex]d{s^2}=-{c^2}d{t^2}+a({t^2})[d{r^2}+{S,k}{(r)^2}d\Omega^2][/itex]
references
(1)"Introductory to Cosmology" Barbera Ryden"
images 1.0,1.1 and 1.2 (see (1))
(2)"Modern Cosmology" Scott Dodelson
(3)"lecture notes, Introductory to Cosmology" Dr. Ka Chan Lu
Last edited:
