Kovac
- 13
- 2
- Homework Statement
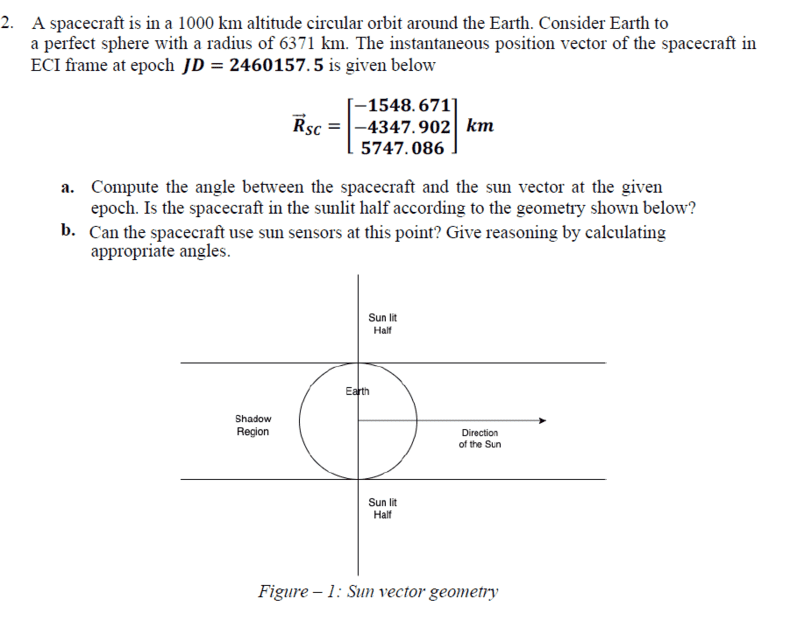
- Compute angle between space craft & sun vector
- Relevant Equations
- .
Hi, so I have no clue how to solve this problem but I started off by rewriting the issue as a dot product to find the angle. So;
cos(θ)= RSC⋅RSun / ∣RSC∣⋅∣RSun∣
Where Rsc = space crafts position vector.
Rsun is the Suns position vector.
∣RSC∣ is the length of the spacecrafts position vector.
∣RSun∣ is the length of the Suns position vector.
So in order to get the angle I planned to take arccosine.
But how do I get Rsun?
Is this a correct approach?
Am I doing something wrong or maybe there's a better approach to the problem?
cos(θ)= RSC⋅RSun / ∣RSC∣⋅∣RSun∣
Where Rsc = space crafts position vector.
Rsun is the Suns position vector.
∣RSC∣ is the length of the spacecrafts position vector.
∣RSun∣ is the length of the Suns position vector.
So in order to get the angle I planned to take arccosine.
But how do I get Rsun?
Is this a correct approach?
Am I doing something wrong or maybe there's a better approach to the problem?