Calculate Natural frequency of a vibrator

[Pivskid]

I have a construction of a vibrator (industrial use).
I should be able to calculate the natural frequency, by means of Hooke's law.
Since I have a physical device I already have a "real world" measurement of the Natural frequency.
The problem is: How to calculate it?
I have tried to do some equivalent work, and a calculation that is far of the measured value.
You could say "why calculate when you have the measured value".
The vibrator at hand now, is only a model.
I need to be able to calculate the NF fairly accurate, in order not to demolise the building where the real one is installed )

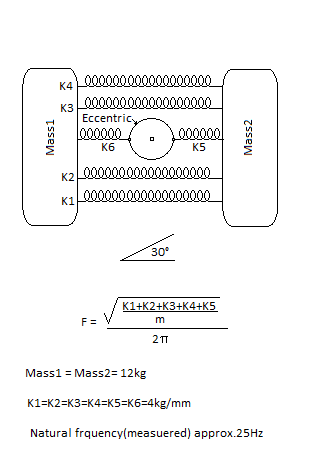
Observe that the 2 mass'es are placed in an angle of 30° from horizontal.
That is..mass2 is higher than mass1.
All springs are equal, eventhough the drawing might insinuate otherwise.

 

[mfb]

What does the central object do?
Are the masses free to move in 2 (or even 3) dimensions? This would make an analytic approach tricky.

A naive ansatz:
Assume that 4kg/mm really means 40N/mm (kg/m is not a meaningful unit for springs).
Replace the 6 springs by an effective spring of (4+1/2)*40N/mm = 180N/mm. Use symmetry to reduce the problem to 1 mass with an effectice spring of D=360N/mm, attached to a fixed end. This gives $f=\frac{1}{2\pi} \sqrt{\frac{D}{m}} = 27.6 Hz$.
Working with g=9.81m/s^2 instead of g=10m/s^2 reduced D by 2% and f by 1%, so the result would be ~27.3Hz. Both values are quite close to the measured frequency.

 

[Pivskid]

The central object, I assume you mean the eccentric, it drives the vibrator.
It is a motor with an eccentric attaached to the shaft.
The 2 masses are moving in one direction (the 30° from horizontal).
I understand how you get the 4kg/mm to 40N/mm, since it is essentially the same.
But then I'm lost.
You replace the 6 springs into 4+½, where does the ½ come from ?
Then you reduces the 2 masses to 1 by symmetry.. how? (mass1+mass2 ?)
And you end up with an equivalent spring twice as high 360N/mm ?

 

[mfb]

4 springs are connecting both masses, they can be added. The two middle springs can be replaced with an effective spring of 20N/mm. If you use 20N of force, you compress both springs by 1/2 mm and therefore the total length reduces by 1mm.

In the same way, a 180N/mm-spring can be replaced by a 360N/mm-spring if I just look at the compression on one side. This is the other direction.

 

[Pivskid]

ohh you see spring K5 and K6 as being in series.
Well there might be a catch to that, since the eccentric is by the propelling motor is attached to the frame.
I still do not get what you did to the mass m in the equation (=240N ?)

I cannot get your formula to result in 27,6Hz (

 

[mfb]

ohh you see spring K5 and K6 as being in series.
Well there might be a catch to that, since the eccentric is by the propelling motor is attached to the frame.

That is no problem, you can consider just one side all the time if that is easier to visualize. There, one spring does not matter at all.

$f=\frac{1}{2\pi} \sqrt{\frac{D}{m}} = 27.6 Hz$

D=360N/mm, m=12kg.
Did you consider the mm <-> m conversion?

 

[Pivskid]

Yes, I let the 360N/mm -> 360kN/m
I now understand you set the mass to 12kg not 120N, in the equation, as I expected.
Ít surprises me a little. Why in kg and not N ?