Calculate the correlation coefficient in the given problem

[chwala]

Homework Statement

see attached

Relevant Equations

stats

Unless there is another alternative method, i would appreciate...ms did not indicate working...thought i should share my working though...

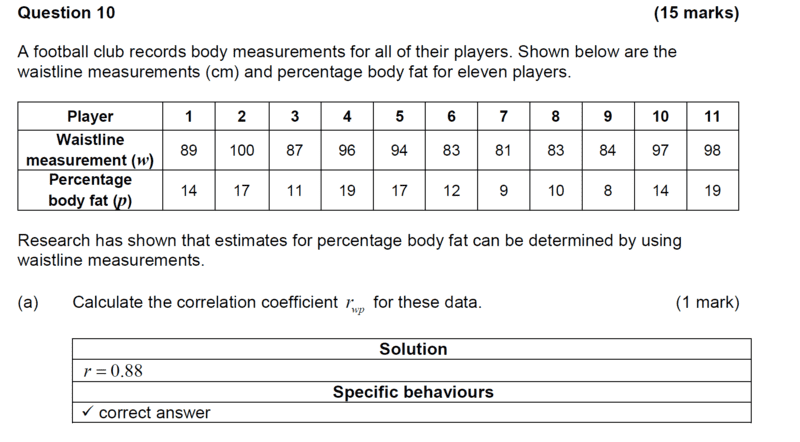
Let Waistline= $X$ and Percentage body fat =$Y$ and we know that $n=11$

$\sum X=992, \sum XY=13,772$ and $\sum Y=150$

Then it follows that,

Correlation coefficient

= $\dfrac{(11×13,772)-992×150}{\sqrt {(11×89,950)-992^2)(11×2,202)-150^2)}}=\dfrac{151,492-148,800}{3045.4379}=\dfrac{2,692}{3045.4379}=0.8839=0.88$ (to two decimal places).

switching $x$ and $y$ would that be appropriate? considered wrong with correct working? ...just asking. By letting $X$ be the Percentage body fat, that is...

...next i would want to determine the equation of least-squares...

Cheers!

 

[Mark44]

switching x and y would that be appropriate? considered wrong with correct working?

I don't believe that switching x and y would be appropriate.

"Estimates for percentage of body fat can be determined by ... waistline measurements."

This statement implies that the independent variable X is the set of waistline measurements, and the dependent variable Y is the set of percentages of body fat.

 

[chwala]

yap...i can from my calculations that the equation of least squares would be given by;

$y=β_1x+β_0$

where,

$β_1=\dfrac{13,772-\frac{992×150}{11}}{89,950-\frac{992×992}{11}}=\dfrac{244.73}{489.64}=0.4998=0.5$ to one decimal place.

$β_0=13.636-(0.4998×90.18)=13.636-45.07=31.43$

thus,$y=0.4998x+31.43=0.5x+31.4$

I noted that if we input,

$0.5$ instead of $0.4998$ in the equation, $β_0=13.636-(0.5×90.18)=13.636-45.09=31.454$
which rounds to $-31.5$(to one decimal place) which is not as is indicated on ms below. At what point does one round off? or rather what $β_1$ value should one use?

Mark scheme solution

cheers!

 

[Mark44]

yap...i can from my calculations that the equation of least squares would be given by;
$y=β_1x+β_0$
where,
$β_1=\dfrac{13,772-\frac{992×150}{11}}{89,950-\frac{992×992}{11}}=\dfrac{244.73}{489.64}=0.4998=0.5$ to one decimal place.
$β_0=13.636-(0.4998×90.18)=13.636-45.07=31.43$

Sign error above. That last number should be -31.43.

thus,
$y=0.4998x+31.43=0.5x+31.4$

I noted that if we input,
$0.5$ instead of $0.4998$ in the equation, $β_0=13.636-(0.5×90.18)=13.636-45.09=31.454$
which rounds to $-31.5$(to one decimal place) which is not as is indicated on ms below. At what point does one round off? or rather what $β_1$ value should one use?

There are different rules about rounding when the digit following the digit to round is 5. One rule says that if the digit to be rounded, round towards an even digit in the digit in front of that one. So, using this rule, -31.45 would round to -31.4 while -31.35 would round to -31.4.

 

[WWGD]

Yes, correlation is,symmetric; Corr(X,Y)=Corr( Y,X).
But , regarding the line of best fit Y^=m^x ×b^
you can't just solve for X to get the best fit between Y and X. For one, if Y depends on X, it doesn't follow that X depends on Y; consider for one Y= height, X = age.

 

[chwala]

Yes, correlation is,symmetric; Corr(X,Y)=Corr( Y,X).
But , regarding the line of best fit Y^=m^x ×b^
you can't just solve for X to get the best fit between Y and X. For one, if Y depends on X, it doesn't follow that X depends on Y; consider for one Y= height, X = age.

Meaning that we can indeed switch $x$ and $y$ in determining the correlation coefficient. I will check on this ... cheers @WWGD

 

[WWGD]

I believe correlation is the inner-product in a space of Random Variables. Will double check on that.

 

[chwala]

I don't believe that switching x and y would be appropriate.

"Estimates for percentage of body fat can be determined by ... waistline measurements."

This statement implies that the independent variable X is the set of waistline measurements, and the dependent variable Y is the set of percentages of body fat.

Your statement seems to be correct.