SchroedingersLion
- 211
- 56
- TL;DR
- Question to a derivation in the book "An Introduction to Statistical Mechanics and Thermodynamics" by R. H. Swendsen (second edition).
Greetings!
I started working through a book of statistical mechanics, and I struggle with properly deriving a formula that makes intuitive sense. I will describe the situation and then my own solution attempts.
Suppose we have two systems ##j## and ##k## of volumes ##V_j## and ##V_k## and particle numbers ##N_j## and ##N_k##. The particles do not interact. The systems are isolated from each other. Suppose we are given the total energy ##E## and we are interested in the probability distribution ##P(E_j, E_k)## where ##E_j + E_k = E = const##. We make the assumption that all particle momenta are equally likely, but they satisfy the constraint ## E=\sum_i^N \frac{p_i^2}{2m} ##, where ##p_i## is the momentum of the ##i-th## particle, ##m## the particle mass, and ##N=N_j + N_k##. The same energy-momentum relation holds in each subsystem.
Now consider this section that the author allegedly makes use of:
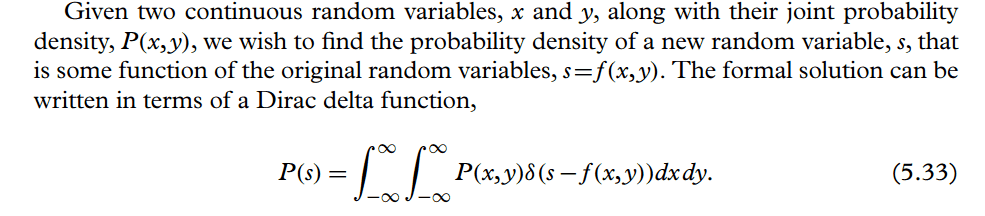
I already found a heuristic proof for this, so let's accept this as a given fact.
Now he wants to derive the distribution of the two energies from the momenta making use of (5.33). He writes:
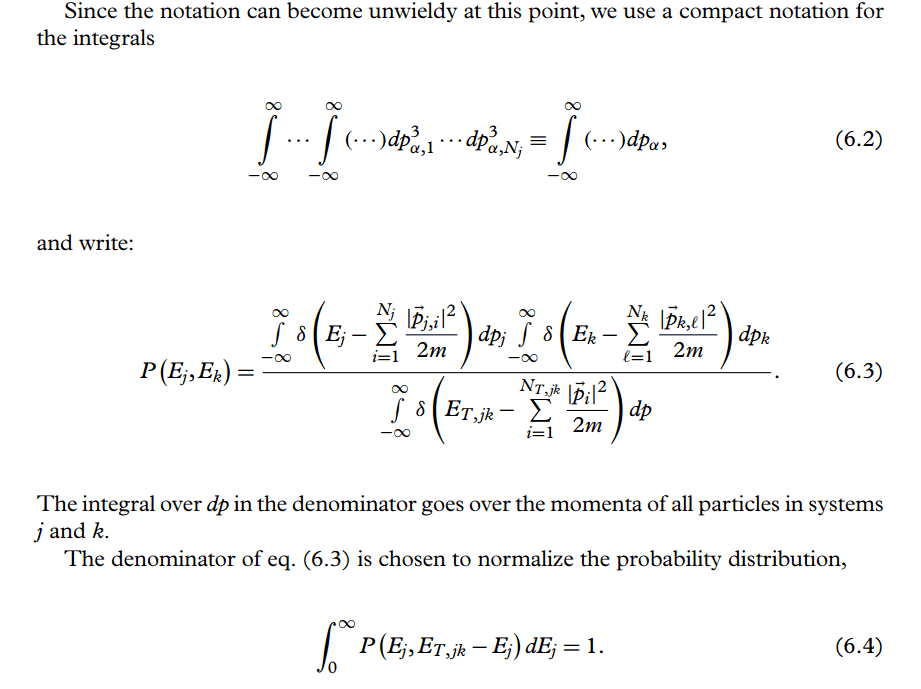
---
I don't understand how he actually ended up at (6.3). Given (5.33), what we can write is
$$\begin{align}
p_{E_j}(E_j) & = \int_{-\infty}^{\infty} p_{p_j}(p_{j,1},p_{j,2},...) \delta \left( E_j - \sum_{i}^{N_j} \frac{p_{j,i}^2}{2m} \right) \, dp_j , \\
p_{E_k}(E_k) &= \int_{-\infty}^{\infty} p_{p_k}(p_{k,1},p_{k,2},...) \delta \left( E_k - \sum_{i}^{N_k} \frac{p_{k,i}^2}{2m} \right) \, dp_k,
\end{align}$$
where ##p_{p_x}## and ##p_{E_x}## are the distributions of momenta and energies in system ##x##.
The joint distribution of all momenta should be writable as
$$
p(p_{1}, p_{2},...) = \frac{ \delta \left( E- \sum_i^N \frac{p_i^2}{2m}\right) } {\int_{-\infty}^{\infty} \delta \left( E- \sum_i^N \frac{p_i^2}{2m}\right) \, dp}.
$$
Now, all the delta functions are there, one just has to combine them properly...
It is clear that ##P(E_j, E_k) \neq p_{E_j}(E_j) p_{E_k}(E_k)## (since the energies in the subsystems are linearly dependent, i.e. fully correlated). In the same way, the joint momentum distribution cannot be written as a product of the joint distributions in the subsystems...
It is also clear that ##p_{E_k}(E_k) = p_{E_j}(E-E_k) ##.
If one interprets the delta-"functions" as living under energy integrals, one can also write
$$
\delta \left( E- \sum_i^N \frac{p_i^2}{2m}\right) = \delta \left( E_j - \sum_{i}^{N_j} \frac{p_{j,i}^2}{2m} \right)\delta \left( E_k - \sum_{i}^{N_k} \frac{p_{k,i}^2}{2m} \right). $$
Any idea from here?
I am always frustrated by the lack of derivations and / or mathematical rigor in physics books. I spent more time thinking about derivations such as these than actually learning the physics...
I started working through a book of statistical mechanics, and I struggle with properly deriving a formula that makes intuitive sense. I will describe the situation and then my own solution attempts.
Suppose we have two systems ##j## and ##k## of volumes ##V_j## and ##V_k## and particle numbers ##N_j## and ##N_k##. The particles do not interact. The systems are isolated from each other. Suppose we are given the total energy ##E## and we are interested in the probability distribution ##P(E_j, E_k)## where ##E_j + E_k = E = const##. We make the assumption that all particle momenta are equally likely, but they satisfy the constraint ## E=\sum_i^N \frac{p_i^2}{2m} ##, where ##p_i## is the momentum of the ##i-th## particle, ##m## the particle mass, and ##N=N_j + N_k##. The same energy-momentum relation holds in each subsystem.
Now consider this section that the author allegedly makes use of:
I already found a heuristic proof for this, so let's accept this as a given fact.
Now he wants to derive the distribution of the two energies from the momenta making use of (5.33). He writes:
---
I don't understand how he actually ended up at (6.3). Given (5.33), what we can write is
$$\begin{align}
p_{E_j}(E_j) & = \int_{-\infty}^{\infty} p_{p_j}(p_{j,1},p_{j,2},...) \delta \left( E_j - \sum_{i}^{N_j} \frac{p_{j,i}^2}{2m} \right) \, dp_j , \\
p_{E_k}(E_k) &= \int_{-\infty}^{\infty} p_{p_k}(p_{k,1},p_{k,2},...) \delta \left( E_k - \sum_{i}^{N_k} \frac{p_{k,i}^2}{2m} \right) \, dp_k,
\end{align}$$
where ##p_{p_x}## and ##p_{E_x}## are the distributions of momenta and energies in system ##x##.
The joint distribution of all momenta should be writable as
$$
p(p_{1}, p_{2},...) = \frac{ \delta \left( E- \sum_i^N \frac{p_i^2}{2m}\right) } {\int_{-\infty}^{\infty} \delta \left( E- \sum_i^N \frac{p_i^2}{2m}\right) \, dp}.
$$
Now, all the delta functions are there, one just has to combine them properly...
It is clear that ##P(E_j, E_k) \neq p_{E_j}(E_j) p_{E_k}(E_k)## (since the energies in the subsystems are linearly dependent, i.e. fully correlated). In the same way, the joint momentum distribution cannot be written as a product of the joint distributions in the subsystems...
It is also clear that ##p_{E_k}(E_k) = p_{E_j}(E-E_k) ##.
If one interprets the delta-"functions" as living under energy integrals, one can also write
$$
\delta \left( E- \sum_i^N \frac{p_i^2}{2m}\right) = \delta \left( E_j - \sum_{i}^{N_j} \frac{p_{j,i}^2}{2m} \right)\delta \left( E_k - \sum_{i}^{N_k} \frac{p_{k,i}^2}{2m} \right). $$
Any idea from here?
I am always frustrated by the lack of derivations and / or mathematical rigor in physics books. I spent more time thinking about derivations such as these than actually learning the physics...