SUMMARY
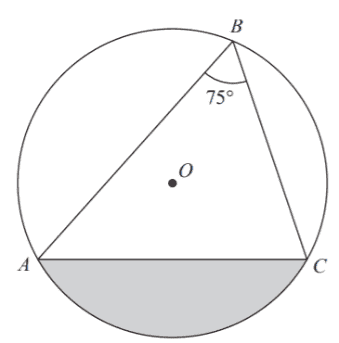
The discussion focuses on calculating the radius of a circle given specific parameters, including angle ABC at 75 degrees and a shaded segment area of 200 cm². The relationship between the areas of sector AOC and triangle AOC is established, leading to an equation for the radius (r). The area of sector AOC is determined to be (5πr²)/12, while the area of triangle AOC is derived using trigonometric functions, ultimately allowing for the calculation of r by setting the difference between these areas equal to 200 cm².
PREREQUISITES
- Understanding of circle geometry and properties
- Knowledge of trigonometric functions (sine and cosine)
- Familiarity with area calculations for sectors and triangles
- Ability to solve equations involving variables
NEXT STEPS
- Study the derivation of the area of a sector in a circle
- Learn about the properties of isosceles triangles and their area calculations
- Explore the application of trigonometric identities in geometry
- Practice solving equations involving multiple variables
USEFUL FOR
Students and educators in geometry, mathematicians focusing on circle properties, and anyone interested in applying trigonometry to solve geometric problems.