Calculate the volume of the set M

[mathmari]

Hey! :giggle:

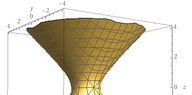
We have the set $M=\{(x,y,z)\in \mathbb{R}^3 : x^2+y^2-z^2\leq 1, \ 0 \leq z\leq 3\}$. Draw $M$ and calculate the volume of $M$.


I have done the following :

\begin{equation*}\int_M\, dV=\int\int\int\, dx\, dy\, dy\end{equation*} Which are the boundaries of the integrals? Do we have to use spherical coordinates?

Or do we set $x=r\cos\theta$ and $y=r\sin\theta$ and $z$ remains $z$ with $0\leq z\leq 3$ ?
We have that $x^2+y^2-z^2\leq \Rightarrow r^2-z^2\leq 1 \Rightarrow r^2\leq 1+z^2 \Rightarrow -\sqrt{1+z^2}\leq r\leq \sqrt{1+z^2}$ and since $r$ is the radius and so it must be positive we get $0 \leq r\leq \sqrt{1+z^2}$, right? But what about $\theta$ ?

Or is there an other way to calculate that?

:unsure:

 

[I like Serena]

Hey mathmari!

It's called cilindrical coordinates.
$\theta$ goes all the way around and is between 0 and $2\pi$.

 

[mathmari]

It's called cilindrical coordinates.
$\theta$ goes all the way around and is between 0 and $2\pi$.

So the boundaries are $0 \leq r\leq \sqrt{1+z^2}$, $0\leq z\leq 3$ and $0\leq \theta\leq 2\pi$, right?

So do we have so far the following?
\begin{align*}\int_M\, dV=\int_0^3\int_0^{\sqrt{1+z^2}}\int_0^{2\pi}\, d\theta \, dr\, dz=\int_0^3\int_0^{\sqrt{1+z^2}}\left [\theta\right ]_0^{2\pi} \, dr\, dz=\int_0^3\int_0^{\sqrt{1+z^2}}2\pi \, dr\, dz=\int_0^32\pi \left [r\right ]_0^{\sqrt{1+z^2}}\, dz=\int_0^32\pi\sqrt{1+z^2} \, dz\end{align*}

:unsure:

How do we know that $\theta$ goes all the way around? Is it because we don't have any restriction? :unsure:

 

[I like Serena]

So the boundaries are $0 \leq r\leq \sqrt{1+z^2}$, $0\leq z\leq 3$ and $0\leq \theta\leq 2\pi$, right?

So do we have so far the following?

It should be
\begin{align*}\int_M\, dV=\int_0^3\int_0^{\sqrt{1+z^2}}\int_0^{2\pi}\, r\, d\theta \, dr\, dz\end{align*}
An infinitesimal volume element in cylindrical coordinates is $r\, d\theta \, dr\, dz$.
Or put otherwise, the absolute value of the Jacobian determinant is $r$.

How do we know that $\theta$ goes all the way around? Is it because we don't have any restriction?

Indeed.
We should be able to see it in a drawing.

 

[mathmari]

We should be able to see it in a drawing.

With which programm can I draw that? :unsure:

I tried with Geogebra, but it doesn't work, maybe I write the input in a wrong way.

:unsure:

 

[I like Serena]

With which programm can I draw that? :unsure:

I tried with Geogebra, but it doesn't work, maybe I write the input in a wrong way.

Wolfram gives me:

In Geogebra 3D, I could make:

I used Tools / Intersect to intersect the hyperboloid and the planes.

 

[mathmari]

Wolfram gives me:
View attachment 11317


In Geogebra 3D, I could make:

View attachment 11318

I used Tools / Intersect to intersect the hyperboloid and the planes.

Ah to plot that do we use $x^2+y^2-z^2=1$ instead of $x^2+y^2-z^2\leq 1$ ? :unsure:

 

[I like Serena]

Ah to plot that do we use $x^2+y^2-z^2=1$ instead of $x^2+y^2-z^2\leq 1$ ?

I guess so. Geogebra doesn't seem to like the $\le$. :unsure: