Calculating a force on a piston

[Auto Engineer]

I have what I think for me is an interesting subject, which deserves some thought about how to correctly calculate the force acting on a Otto cycle piston, and whether that force is from compression pressure, or the force acting from the crank and conrod.

You have an engine running and diagnostic equipment displays that the engine cylinder torque on one cylinder is 26Nm, the rest are significantly different just for arguments sake.

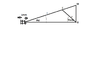
The engine does not run smoothly and a diagnosis involves calculating the force Fp on the piston at 1mm before TDC.

You are given the following data;

I = 70mm
r = 18mm
T = 26 Nm
θ = 17.13°
∅ = 4.34°

Using the sine rule I calculated that "I" is indeed 70mm by the following method;

I / sin I = P / sin P = I / sin(17.13) = 18 / sin(4.34) = 70.06mm

I used Pythagoras theorem to calculate the length OP = 68mm

The radius OC is given at 18mm, which is the same length as OM being also the radius.

I was suprised to find after calculating the length OP that the diagram seems incorrect, although any triangle which has a right angle will have a longest side known as the hypotenuse, but this diagram does not indicate a right angle, and I would not expect it to because we are talking about a rotating mechanism.

The answer/solution to the problem is given as Fp = 3935 N

This is how I worked out the problem;

Triangle OCM = ∅ + θ = 21.47°

Angle LM = 85.66°

OM = 18(sin 21.47) / (sin 85.66) = 6.61

Force on piston Fp = 26 / 6.61 x 1000 = 3933 N

Is there another way of calculating the force, and is this force acting on top of the piston or through the crank and conrod to the piston?

Any help appreciated

 

[anorlunda]

You are oversimplifying. Multiple forces act on the piston. They all vary with time. Conditions in the chamber are non-equilibirium. I do not think that simple equations will ever do what you want.