Understanding and Troubleshooting Handlebar Load Calculations

[nateTheaweseome]

TL;DR Summary

Calculated handle bar pulling force to be significantly lower than what I measured in real life; This is attached to 2 brake cables, each connected to one end of a gas piston (tension).

Hey all,

I'm either overthinking it or too tired but this problem should be an easy one to figure out but I'm stumped embarrassingly.

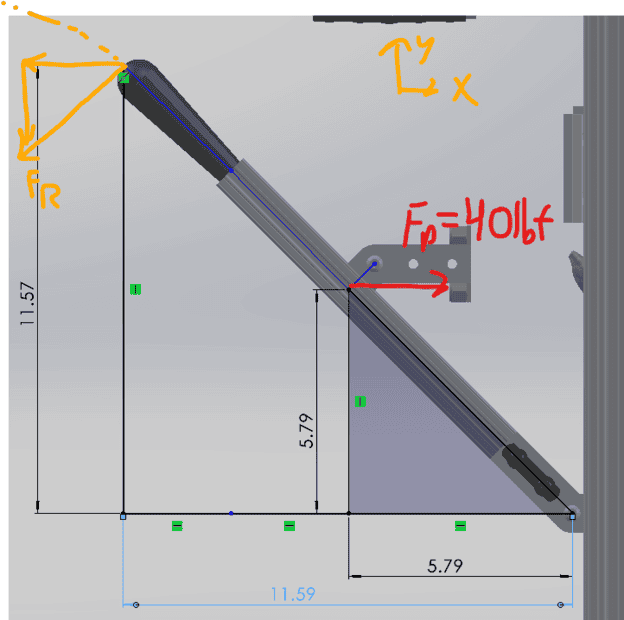
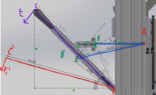
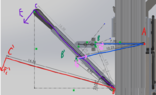
Say in the photo above is a lever arm. I'm trying to backtrack to calculate the force a user must input (yellow) against a force (red). It can pivot around the hinge, and when I calculate the Fr by summing moments around the pivot and solving for Fr, I get around 14lbf. This is designed so that Fp stays horizontal for the range of motion on the arm (not meant to go completely flat).

Now, this doesn't make sense because in real life, I measured this to be about 70lbf...Granted, several things could be wrong here:
1. I screwed up my moment equation (the 40lbf doesn't have a component in Y does it?)
2. I'm thinking this the wrong way
3. The Fp value is wildly wrong. It's a long story but TL;DR That force is coming from 2 different brake cables, attached to both ends of a tension gas piston (rated at 20lbf compression, 34lbf extension). The way I got 40lbf is that when the gas piston is not displaced, the force is around 20lbf, and multiply that by 2 since there's two brake cables attached to both ends of the piston, so the lever at the mounting point will see 40lbf. Now as I understand the compression force increases as displacement increases like a spring but even when I change the total Fp value to be 68lbf, it's no where near what I measured in real life.

I'm kinda stumped so any help would be great.

 

[.Scott]

I will try to get you on the right path without just giving you any answers.
As I understand it, the pistons and brake cables are not shown in the diagram.

Foot-pounds are units of energy, not force.
So, I am suspecting you are not describing the problem perfectly.
I suggest that when you are working with work or energy, you use a letter other than F.

If 40 foot-pounds of work is applied to the cables, you should expect 40 foot-pounds applied to the lever - presuming, of course, that the device is properly lubricated.

 

[Baluncore]

Foot-pounds are units of energy, not force.

The lbf = pound⋅foot can be an energy unit, or an engineering moment = a physics torque.
In this case it is specified to be a moment, which is a circular force.
The SI unit of torque is the N⋅m .

 

[Baluncore]

Where is the pivot or hinge in the diagram?
Where are the points of attachment to the tension gas piston.
The 40 lbf shown in red is not being applied tangentially to the lever pivot, so it is not a torque.
Am I correct in thinking that lbf here stands for 40 "pounds force" ?

 

[nateTheaweseome]

Where is the pivot or hinge in the diagram?
Where are the points of attachment to the tension gas piston.
The 40 lbf shown in red is not being applied tangentially to the lever pivot, so it is not a torque.
Am I correct in thinking that lbf here stands for 40 "pounds force" ?

The pivot is at Point A.

The point of attachment to the brake cables, which is connected to the gas piston is what Fb represents. It's really attached to that hinged point that Fb goes across.

40lbf in red has a height displacement of 5.79"...I imagined that if I drew a dotted line across this force vector, it would create a moment around A (Fb * 5.79). Just like if I decomposed Fp into Fpx and Fpy vectors, Fpx would create a moment about A.

Yeah that was what I was thinking for 40 pounds force...was I wrong for the units?

 

[nateTheaweseome]

I will try to get you on the right path without just giving you any answers.
As I understand it, the pistons and brake cables are not shown in the diagram.

Foot-pounds are units of energy, not force.
So, I am suspecting you are not describing the problem perfectly.
I suggest that when you are working with work or energy, you use a letter other than F.

If 40 foot-pounds of work is applied to the cables, you should expect 40 foot-pounds applied to the lever - presuming, of course, that the device is properly lubricated.

Thanks for helping.

The pistons/brake cables are represented by the horizontal force Fb in the new drawing.

Yeah maybe I am unclear about the units here. This is the gas piston, and the "Compression Force, lbs" is 20.

 

[erobz]

So there is a gas cylinder (strut) where the purple arrow is?

 

[nateTheaweseome]

View attachment 335958

So there is a gas cylinder (strut) where the purple arrow is?

Well, being specific, there are two brake cables (sketched out in green). Each brake cable is mounted to a different end on the gas piston (red rectangle). The functionality of this arm is that when you pull down, it'll force the gas piston to separate/expand, and when you release, it'll automatically close.

 

[erobz]

View attachment 335959
Well, being specific, there are two brake cables (sketched out in green). Each brake cable is mounted to a different end on the gas piston (red rectangle). The functionality of this arm is that when you pull down, it'll force the gas piston to separate/expand, and when you release, it'll automatically close.

Please draw the extended cylinder in its orientation. I'm having trouble imagining how you (efficiently) extend the cylinder in the vertical direction by applying a lateral force.

 

[nateTheaweseome]

Please draw the extended cylinder in its orientation. I'm having trouble imagining how you (efficiently) extend the cylinder in the vertical direction by applying a lateral force.

Should've made it more clearer my bad.

The piston is mounted horizontally, on two steel extrusions, riding on 2 linear bearings (you can see the top roller rail in the photo). The gas piston will automatically have the extrusions stay closed, but when I pull on the lever, it forces the gas piston to extend out, thus opening the steel extrusions.

Brake cable is rigidly mounted at two points near the lever arm and the steel extrusion (not shown in the photo), allowing me to make this movement. It works since it's already built, but the pulling force is ridiculous so I'm trying to improve it.

 

[erobz]

View attachment 335960
Should've made it more clearer my bad.

The piston is mounted horizontally, on two steel extrusions, riding on 2 linear bearings (you can see the top roller rail in the photo). The gas piston will automatically have the extrusions stay closed, but when I pull on the lever, it forces the gas piston to extend out, thus opening the steel extrusions.

Brake cable is rigidly mounted at two points near the lever arm and the steel extrusion (not shown in the photo), allowing me to make this movement. It works since it's already built, but the pulling force is ridiculous so I'm trying to improve it.

I'm sorry, this is hard to get my head around (maybe someone else can see it). The cables wrap around the outside of that frame? Give us a top view.

EDIT: Really, lets just be thorough have the standard engineering views.

 

[nateTheaweseome]

I'm sorry, this is hard to get my head around (maybe someone else can see it). The cables wrap around the outside of that frame? Give us a top view.

Not sure if the top down view will help lol but I also included an iso view. The black cable was a crude attempt to model the length of the brake cable but I highlighted it in green anyways.

The blue stars represent where the brake cable fittings are rigidly mounted.

 

[erobz]

View attachment 335961
View attachment 335963

Not sure if the top down view will help lol but I also included an iso view. The black cable was a crude attempt to model the length of the brake cable but I highlighted it in green anyways.

The blue stars represent where the brake cable fittings are rigidly mounted.

OK, I see it. So, what is the tension in each cable ignoring friction in the cable housing?

 

[nateTheaweseome]

OK, I see it. So, what is the tension in each cable ignoring friction in the cable housing?

So my thought process was, if the compression force initially is 20lbs when the assembly is closed, the tension in each cable housing would be 20lbs (gradually increasing to 34lbs once max stroke is hit).

Thus, the lever arm would see double that, which is why I initially chose 40lbs.

 

[erobz]

View attachment 335964
So my thought process was, if the compression force initially is 20lbs when the assembly is closed, the tension in each cable housing would be 20lbs (gradually increasing to 34lbs once max stroke is hit).

Thus, the lever arm would see double that, which is why I initially chose 40lbs.

The way I see it keeps the parts closed with 20 lbf.

then as you apply load, each cable increases to 34 lbf at full extension:

 

[nateTheaweseome]

The way I see it keeps the parts closed with 20 lbf.

View attachment 335965

then as you apply load, each cable increases to 34 lbf at full extension:

View attachment 335967

Okay so it sounds like the force value I chose (40lbf initially for the lever arm since each brake cable is mounted to that hinge) was on the right track then.

So it sounds like my calculations for the pulling force was wrong by setting up my moments incorrectly?

 

[erobz]

Okay so it sounds like the force value I chose (40lbf initially for the lever arm since each brake cable is mounted to that hinge) was on the right track then.

So it sounds like my calculations for the pulling force was wrong by setting up my moments incorrectly?

Not there yet...What is the tension in each cable at in the fully extended position? Your end goal is to fully open them correct?

 

[nateTheaweseome]

Not there yet...What is the tension in each cable at in the fully extended position? Your end goal is to fully open them correct?

For each brake cable at fully extended position, wouldn't it be 34lbs?

 

[erobz]

For each brake cable at fully extended position, wouldn't it be 34lbs?

Yeah, so $F_b$ ( acting on the lever arm ) in the fully extended position is?

 

[nateTheaweseome]

Yeah, so $F_b$ ( acting on the lever arm ) in the fully extended position is?

68lbf correct?

 

[erobz]

Yeah, that's approximate. To be accurate, in the fully extended position draw the forces ( magnitude 34 lbf each ) acting as they actually act on the lever w.r.t. direction and point of application.

 

[nateTheaweseome]

Yeah, that's approximate. To be accurate, in the fully extended position draw the forces ( magnitude 34 lbf each ) acting as they actually act on the lever w.r.t. direction and point of application.

So then ignoring the geometry of the arm (I just realized this is the position of the arm with 20lbf AKA piston closed; when I pull on the lever the angle/lengths will change), is the force decomposition correct?

I am primarily concerned about the decomp for Fb. Say the arm in the snapshot is with the piston has reached full stroke and is seeing ~68lbf of tension. When I sum the moments about A, would it make sense to include Fby?

I say yes but just want to double check my setup.

 

[erobz]

So then ignoring the geometry of the arm (I just realized this is the position of the arm with 20lbf AKA piston closed; when I pull on the lever the angle/lengths will change), is the force decomposition correct?

I am primarily concerned about the decomp for Fb. Say the arm in the snapshot is with the piston has reached full stroke and is seeing ~68lbf of tension. When I sum the moments about A, would it make sense to include Fby?

I say yes but just want to double check my setup.
View attachment 335971

No, you want to decompose forces normal and parallel to their lines of action.

The important component of $F_B$ is the component normal to the line of action $r_{B/A}$ when summing torques about $A$.

Just to be clear what you are doing (not taking into account both tensile forces and where they are applied) is less precise. In my opinion there is very little reason to do it half assed when you have all the geometry (3D model) already worked out. But its ultimately your call, just noting that junk in usually equals junk out.

 

[nateTheaweseome]

No, you want to decompose forces normal and parallel to their lines of action.

View attachment 335975

The important component of $F_B$ is the component normal to the line of action $r_{B/A}$ when summing torques about $A$.

Just to be clear what you are doing (not taking into account both tensile forces and where they are applied) is less precise. In my opinion there is very little reason to do it half assed when you have all the geometry (3D model) already worked out. But its ultimately your call, just noting that junk in usually equals junk out.

That's fair. I guess I just wanted to do something quick but you brought up a good point.

So based off what you suggested, I sketched out two positions of the arm (Red and Purple represents the 40lbf and 68lbf positions respectively).

Point A is where the end brake cable fitting is secured, and so as the lever is pulled the cable will elongate and rotate about this point. Each Brake Cable max stroke is 3" (essentially meaning a total of 6" displacement on the gas piston).

Point C and C' represents where I'm roughly assuming the brake cable load is. Line $r_{C/A}$ and Line $r_{C'/A}$ represents the actual brake cable line (you can see initially the distance is 7.2" and after max stroke it's 10.2").

Brown vectors represent the cable forces in the normal/tangential directions across the line of action between $r_{C/D}$ and $r_{C'/D}$

...So aside from the generalized 68lbf at C/C', would you say this is a decent setup for determining the moments around D?

 

[erobz]

This is what you should be doing:

Figure out this geometry at the furthest position, where the force is the highest.

The cables pass through separate gromets at some distance, so it is not true that the forces are colinear. You can pull all the geometry directly from your model. Figure out what the dashed vectors are in magnitude, and multiply them by their respective moment arms $|| \vec{r}_{B/A}||$, and $|| \vec{r}_{B/A}||$, that's the resisting torque to $F_p$ at its moment arm $|| \vec{r}_{P/A}||$.

 

[jack action]

These gas springs act also as gas dampers:

Gas springs as dampers

One thing you'll notice about gas springs is that they work slowly and smoothly. The end of the piston is designed so the fluid inside the cylinder (gas and liquid) can flow through or around it very slowly. Different springs are designed in various different ways and some pistons are arranged so the fluid will flow more quickly past them when the spring moves in one direction than when it moves the opposite way. For example, when the piston is compressed into the cylinder, the end of the piston may be designed to close up a valve so fluid can flow through it only very slowly, reducing the speed at which the piston can move. When the piston moves the other way, the valve can be designed to open up so fluid will travel past it more quickly, allowing the piston to move much faster. Gas springs are usually designed with a particular size of load in mind so they expand very smoothly at a particular rate (so many centimeters or inches per second).

So the fully compressed force may be 20 lb and the fully extended force may be 34 lb, but the force of the moving piston in between can be much much greater. Damping depends on piston velocity.

Does your 70-lb force stabilize to a lower value when holding the piston still?

 

[erobz]

These gas springs act also as gas dampers:So the fully compressed force may be 20 lb and the fully extended force may be 34 lb, but the force of the moving piston in between can be much much greater. Damping depends on piston velocity.

Does your 70-lb force stabilize to a lower value when holding the piston still?

Fair point, but note that the OP is struggling to calculate equilibrium forces at this time...

I'll step out of the way.

 

[nateTheaweseome]

Fair point, but note that the OP is struggling to calculate equilibrium forces at this time...

I'll step out of the way.

Well thank you for clarifying this for me though.

 

[nateTheaweseome]

These gas springs act also as gas dampers:So the fully compressed force may be 20 lb and the fully extended force may be 34 lb, but the force of the moving piston in between can be much much greater. Damping depends on piston velocity.

Does your 70-lb force stabilize to a lower value when holding the piston still?

I will need to try that out next time I'm working on the device.