Calculating joint reaction forces

[Haku]

Homework Statement

If the joint reaction force at the ankle in the x direction is -125N, calculate the joint reaction force at the knee in the x direction (assuming those are the only two horizontal forces acting on it)

Relevant Equations

Summation

I have this question in my biomechanics class, and the way the teacher has solved it raised some questions with me.
This is the snippet of work from the lecture slides:

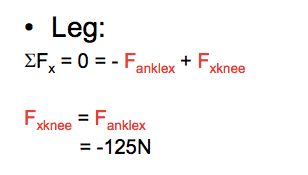
But, if we see the red variables acting as 'placeholders' for the value of respective forces, and the value of the force at the ankle in x direction is -125N.
When summing all ankle forces in x direction it looks like the direction is accounted for twice, because what the summation is if you leave the variables as placeholders for the actual values is:

Fax + Fkx = 0.

=>

Fkx = -Fax = -(-125N) = 125N.

What I get from the calculation done in the picture is the following:

-Fax + Fkx = 0

<=>

-(-125N) + Fkx = 0

=>

Fkx = -125N

But in this case, you have applied the direction of the joint reaction force at the ankle twice right?
Which calculation is correct? Imo the former calculation is more mathematically sound, but I am not sure since it is contradictory to calculation given in class.

 

[haruspex]

I would not describe it as having applied a force twice. Rather, it is a confusion over how the positive direction has been defined.
Where it is clear that two forces will act in opposite directions, it is not unusual to define each to be positive in the direction it will act. That would give the summation equation in the snippet, but in that model the value should have been inserted as +125N.

Since the given force is specified as negative, it is more natural to use the same direction as positive for all forces. That leads to Fax + Fkx = 0, so, again, an answer of +125N.

 

[Haku]

I would not describe it as having applied a force twice. Rather, it is a confusion over how the positive direction has been defined.
Where it is clear that two forces will act in opposite directions, it is not unusual to define each to be positive in the direction it will act. That would give the summation equation in the snippet, but in that model the value should have been inserted as +125N.

Since the given force is specified as negative, it is more natural to use the same direction as positive for all forces. That leads to Fax + Fkx = 0, so, again, an answer of +125N.

Right, but we don't know the direction of force for Fkx. We just know that they are static, so ma = 0. Hence the sum of the forces is 0.
So should it just be Fax + Fkx = 0, then since we know Fax = -125N we can solve for Fkx right?

 

[haruspex]

Right, but either way, with Fax defined as -125N, the resulting Fkx should be +125N right?

Yes.