Calculating Norm of Prime Ideal p = (3, 1 - √-5)

[Firepanda]

I need to calculate the norm of the ideal

p = (3, 1 - √-5)

All the information I have is that it's a prime ideal.

I managed to calculate the normal of the ideal q = (3, 1 + √-5) (which was 3) by finding a the determinant of a base change matrix by considering an integral basis

Here I'm not sure how to do that (in the other example I managed to show an equivelence relation so that I could find an integral bases)

Here is a similar example with the ideal p₁ = (2, 1 + √-17)

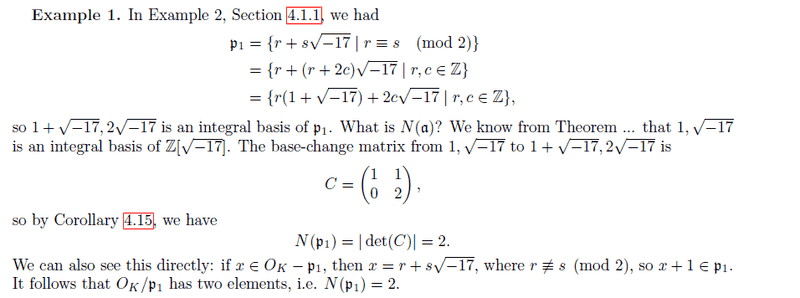
Any help appreciated, thanks.

 

[Hurkyl]

Well, you seem to have been shown two methods: compute a determinant, and compute a residue ring. What difficulty have you had trying to use either method?P.S. when computing the residue ring, I often find it easier to think of your ring as being the quotient of a polynomial ring:

$$\begin{align} \mathbb{Z}[\sqrt{-17}] / (2, 1 + \sqrt{-17}) &\cong \left( \mathbb{Z}[x] / (x^2 + 17) \right) / (2, 1 + x) \\ &\cong \mathbb{Z}[x] / (2, 1+x, x^2 + 17) \\ &\cong \left(\mathbb{Z}[x] / (2)\right) / (1+x, x^2 + 17) \\ &\cong \cdots\end{align}$$