Calculating of currents in a circuit

[Antoha1]

Homework Statement

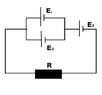
Three e. sources are connected as shown in the diagram.
What is the current flowing through the conductor and the sources when
it is known that E1=1.3 V, E2=1.5 V, E3=2V, r1=r2=r3=0.2 Ω, ($r$)
R=0.55 Ω.

Relevant Equations

Kirchhoff's 1st and 2nd laws;
$V=IR$
I am marking the current flowing through the conductor the same as currect flowing through the E3. (I3)

I am thinking of using Kirchhoff's laws in two contours. 1st contour would be the small one (E1 and E2) counter clock wise. 2nd contour would go through E3,E2,R (wouldn't go through E1).

For 1st contour (CCW):
$E_{1}-E_{2}=r(I_{1}-I_{2})$
2nd contour (CCW):
$E_{3}+E_{2}=I_{3}(r+R)+I_{2}r$
And Kirchhoff's 1st law for left node:
$I_{3}=I_{1}+I_{2}$

Now, that I have system of equations, I can calculate for everyone of them. (only if I applied Kirchhoff's laws correctly, of which I am not sure)
My question is: Did I apply the laws correctly and are these equations OK?

 

[nasu]

It looks OK. You can also try them for some simple case. Like what happens if the two batteries in parallel are identical? Do you get the right result from your equations for this particular case?

 

[Steve4Physics]

It helps to have a diagram with the currents and their (assumed) directions marked.

You can check your work by solving with different loops. I would have chosen:
cell-1 to R to cell-3 back to cell-1 and
cell-2 to R to cell-3 back to cell-2.

You should, of course, get the same final answer whichever loops you use.