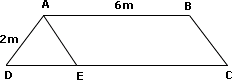
MHB Calculating Perimeter & Area of a Parallelogram & Triangle

Click For Summary
SUMMARY

The discussion focuses on calculating the perimeter and area of geometric shapes, specifically a parallelogram (ABCE) and an equilateral triangle (ADE). The area of a trapezoid (ABCD) is defined using the formula $\dfrac{h}{2}(b_1+b_2)$, where $b_1$ and $b_2$ represent the lengths of the parallel bases. Participants seek clarification on the specific segment CD and its relation to the overall calculations. The perimeter calculation is noted to be straightforward.

PREREQUISITES
  • Understanding of geometric shapes, specifically parallelograms and triangles.
  • Familiarity with the formula for the area of a trapezoid.
  • Basic knowledge of perimeter calculations for polygons.
  • Ability to interpret geometric diagrams and segments.
NEXT STEPS
  • Study the properties and formulas related to parallelograms and triangles.
  • Practice calculating the area and perimeter of various trapezoids.
  • Explore geometric proofs involving the relationships between different shapes.
  • Learn about the applications of these calculations in real-world scenarios.
USEFUL FOR

Students, educators, and anyone interested in geometry, particularly those looking to improve their skills in calculating areas and perimeters of complex shapes.

Abdullah Qureshi
Messages
16
Reaction score
0
Find the perimeter and area of CD, if ABCE is a parallelogram and

ADE is an equilateral triangle.
 

Attachments

  • Parallelogram.png
    Parallelogram.png
    686 bytes · Views: 115
Mathematics news on Phys.org
CD is a line segemnt, ABCD is a trapezoid. Is that what you're trying to find the area & perimeter for?

Perimeter should be rather simple ... what do you get?

Area of a trapezoid is $\dfrac{h}{2}(b_1+b_2)$ where $b_1$ and $b_2$ are the parallel bases.

Where, exactly, are you having trouble?
 

Similar threads

MHB Find length that minimizes the perimeter
  • · Replies 1 ·
Replies
1
Views
1K
MHB [ASK] Find the ratio of the area of triangle BCH and triangle EHD
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad ABC triangle with integer sides
  • · Replies 17 ·
Replies
17
Views
2K
MHB Prove Equal Area Triangle & Parallelogram, $\angle ADC=90^{\circ}$
  • · Replies 9 ·
Replies
9
Views
4K
MHB Need help with parallelogram proof
  • · Replies 1 ·
Replies
1
Views
1K
MHB Problem about equilateral triangles
  • · Replies 2 ·
Replies
2
Views
1K
MHB What is the perimeter of triangle ABC?
  • · Replies 2 ·
Replies
2
Views
5K
MHB What is the perimeter of triangle ABC?
  • · Replies 13 ·
Replies
13
Views
4K
MHB Is there a formula for finding the perimeter of a triangle with known vertices?
  • · Replies 3 ·
Replies
3
Views
2K
MHB What is the Perimeter of Triangle ABC?
  • · Replies 2 ·
Replies
2
Views
2K