Calculating reaction force for sliding plank

[sunquick]

Homework Statement

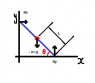
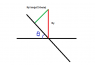
A plank of length 2L leans against a wall. It starts to slip downward without friction. Show that the top of the plank loses contact with the wall when it is at two-thirds of its initial height.
(from Kleppner&Kolenkow,An Introduction to Mechanics 1st ed., problem 6.41)

Homework Equations

Equation of motion for translation of center of mass:

The coordinates of the center of mass are

x = L \cos(\theta)
y= L \sin(\theta)

Differentiating twice with respect to time, the acceleration of CoM is

\ddot{x} = - L \ddot{\theta} \sin(\theta) - L \dot{\theta}^2 \cos(\theta)
\ddot{y} = L \ddot{\theta} \cos(\theta) - L \dot{\theta}^2 \sin(\theta)

So the equations of motion for the center of mass are

m \ddot{x} = - m L \ddot{\theta} \sin(\theta) - m L \dot{\theta}^2 \cos(\theta) = N_x
m \ddot{y} = m L \ddot{\theta} \cos(\theta) - m L \dot{\theta}^2 \sin(\theta) = - m g +N_y

Conservation of energy:
Since there is no friction, energy is conserved and so
m g y_0=\frac{1}{2} m v^2 + \frac{1}{2} I_0 \dot{\theta}^2 + m g y

We can make the following substitutions
I_0 = \frac{1}{3} m L^2
v^2 = \dot{x}^2 + \dot{y}^2 = L^2 \dot{\theta}^2

So we get
m g y_0=\frac{1}{2} m L^2 \dot{\theta}^2 + \frac{1}{6} m L^2 \dot{\theta}^2 + m g L \sin(\theta)

The final equation we need is the angular equation of motion, which we can get making use of the fact that energy is conserved. We can differentiate both sides of the conservation of energy equation and get

0 = m L^2 \dot{\theta} \ddot{\theta} + \frac{1}{3} m L^2 \dot{\theta} \ddot{\theta} + m g L \dot{\theta} \cos(\theta)

Which can be further simplified into
\ddot{\theta} = - \frac{3}{4} \frac{g}{L} \cos(\theta)

One other way to get the angular equation of motion is to balance the torques around the axis of the center of mass
I_0 \ddot{\theta} = N_y L \sin(\theta) - N_x L cos(\theta)

The Attempt at a Solution

I've been able to solve this problem and show what was asked, but I'd like to show you my first atttempt at solving it and understand what I did wrong and why was wrong.

The plank loses contact with the wall when N_x = 0 so from the equation of motion for the x coordinate of the center of mass we get

- m L \ddot{\theta} \sin(\theta) - m L \dot{\theta}^2 \cos(\theta) = 0

And substituting into it \ddot{\theta} = - \frac{3}{4} \frac{g}{L} \cos(\theta) we get the following equation

\dot{\theta}^2 \cos(\theta) - \left( \frac{3}{4} \frac{g}{L} \cos(\theta) \right) \sin(\theta) = 0

which can be solved to

\dot{\theta}^2 = \frac{3 g}{4 L} \sin(\theta)

Knowing \ddot{\theta} and \dot{\theta}^2 I can make use of the equation of motion for the y coordinate of the center of mass and find the force N_y at the instant the plank loses contact with the wall, at which time N_x = 0.

N_y = m g + m L \cos(\theta) \left(- \frac{3 g}{4 L} \cos(\theta) \right) - m L \sin(\theta) \left(\frac{3 g}{4 L} \sin(\theta) \right)
N_y = \frac{1}{4} m g

The torque balance equation then reads

I_0 \ddot{\theta} = N_y L \sin(\theta) = \frac{1}{4} m g L \sin(\theta)
\frac{1}{3} m L^3 (-\frac{3g}{4L} \cos(\theta) ) = \frac{1}{4} m g L \sin(\theta)

Which I then tried to solve to find \theta but ended up with something weird,
- \cos(\theta) = \sin(\theta)
from which I can tell something went wrong along the way, and I suspect it is from finding the N_y force, hence the title of the post.

What did I do wrong? Why is it wrong?

 

[haruspex]

One other way to get the angular equation of motion is to balance the torques around the axis of the center of mass
I_0 \ddot{\theta} = N_y L \sin(\theta) - N_x L cos(\theta)

i believe the signs are wrong. Ny causes an anticlockwise angular acceleration. The way you have defined theta, a positive change is a clockwise rotation.

 

[sunquick]

Thank you for your answer. I think you're right, the signs are indeed wrong. Reversing the signs I get
I_0 \theta = - N_y L \sin(\theta) + N_x L\cos(\theta)

Going through till the end I get
\sin(\theta) = \cos(\theta)
This equation has one solution between 0 and Pi/2, which is Pi/4, but I don't think that's the right answer.

 

[TSny]

One other way to get the angular equation of motion is to balance the torques around the axis of the center of mass
I_0 \ddot{\theta} = N_y L \sin(\theta) - N_x L cos(\theta)

Check to see if you picked the correct trig functions here.

 

[sunquick]

Check to see if you picked the correct trig functions here.

Thank you for replying.
I don't know if the trig functions are correct, because I've tried to do this so many times over and I am really confused.
I'll try to explain my reasoning:

The definition of the x and y coordinates in terms of the angle theta look like polar coordinates, so I reasoned that the torques would come from the components of the forces perpendicular to the plank, and the perpendicular components would be the radial components.

So if we make our basis vectors be
\mathbf{\hat{r}} = \cos(\theta) \mathbf{\hat{i}} + \sin(\theta) \mathbf{\hat{j}}
\mathbf{\hat{\theta}} = - \sin(\theta) \mathbf{\hat{i}} + \cos(\theta) \mathbf{\hat{j}}

Then
\mathbf{N_x} = N_x \cos(\theta) \mathbf{\hat{r}} - N_x \sin(\theta) \mathbf{\hat{\theta}}
\mathbf{N_y} = N_y \sin(\theta) \mathbf{\hat{r}} + N_y \cos(\theta) \mathbf{\hat{\theta}}
\mathbf{W} = -m g \sin(\theta) \mathbf{\hat{r}} - m g \cos(\theta) \mathbf{\hat{\theta}}

I dot each of those forces with the r basis vector, and multiply by L and the sum should be the sum of the torques.

I then tried to do a different type of reasoning and drawed a diagram, which I uploaded. If the diagram is correct, the torque resulting from the N_y reaction force is N_y L \sin(\pi/2 - \theta) = N_y L \cos(\theta) which seems to contradict what I tried before.

 

[TSny]

I don't follow your method using polar coordinates. But your diagram method looks good. It gives you the correct magnitude of the torque due to N_y. You'll need to consider the sign of this torque when setting up your torque equation.