Inneedofhelp
Hello,
I am very new to gears I am fairly confused about planetary gears. I want to know the load on the gears contact point between the sun and the planets and the planets and the ring, assuming the ring not moving. Given I have the solid works file ,the pressure angle, and the gear ratios, I can easily calculate the distances, teeth numbers, etc. I also know the initial driving torque of the sun gear.
So, my question is, utilizing the solid works file and the driving sun gear torque how do I calculate the load on the contact point for each of the gears? Is there a general equation I can use without knowing the power and the rpm?
Thank You

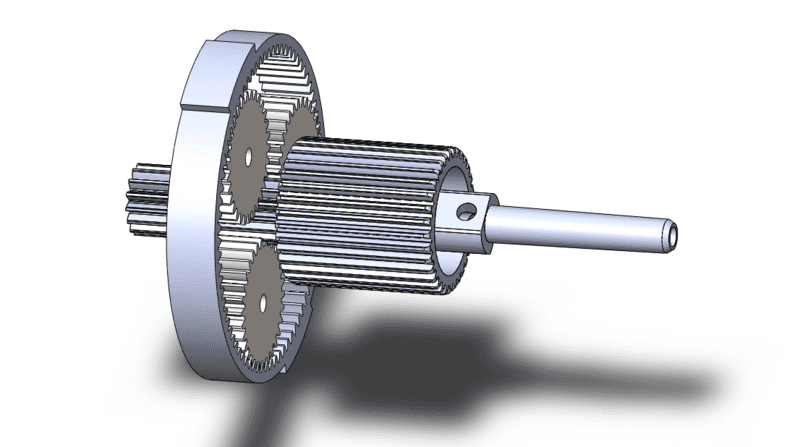
I am very new to gears I am fairly confused about planetary gears. I want to know the load on the gears contact point between the sun and the planets and the planets and the ring, assuming the ring not moving. Given I have the solid works file ,the pressure angle, and the gear ratios, I can easily calculate the distances, teeth numbers, etc. I also know the initial driving torque of the sun gear.
So, my question is, utilizing the solid works file and the driving sun gear torque how do I calculate the load on the contact point for each of the gears? Is there a general equation I can use without knowing the power and the rpm?
Thank You
Last edited by a moderator: