Calculating the Moment of Inertia

In summary, The conversation discusses finding the center of mass and moment of inertia for four masses connected by massless, rigid rods. The coordinates for the center of mass are 0.0517m, 0.0517m. For part b, the equation I=MR^2 is used, with R being the distance from the rotation axis to the mass in question.
  • #1
erok81
464
0

Homework Statement



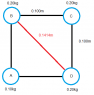
The four masses shown in the attachment are connectec by massless, rigid rods.

a) find the coordinates of the center of mass.
b) find the moment of inertia about a diagonal axis that passes through mass B and D.

Homework Equations



I=MR^2...I think.

The Attempt at a Solution



I've solved part a which ended up being 0.0517m, 0.0517m.

Part b is where I am stumped.

I've tried [tex]I=M_{A}R^{2}_{A}+M_{B}R^{2}_{B}+M_{C}R^{2}_{C}+M_{D}R^{2}_{D}[/tex] using both the radius of the rods as well as the radius of the center of mass, but neither works.

I know I am doing this wrong and it's probably a conceptual thing, but I can't see it. :confused:
 

Attachments

  • Figure One.png
    Figure One.png
    3.2 KB · Views: 429
Physics news on Phys.org
  • #2
The R's in your equation should be the distance from the rotation axis to the mass in question.
 

1. What is the definition of Moment of Inertia?

Moment of Inertia is a measure of an object's resistance to rotational motion. It is the sum of the products of each element's mass and the square of its distance from the axis of rotation.

2. How is Moment of Inertia calculated?

Moment of Inertia is calculated by taking the integral of the mass of each element multiplied by the square of its distance from the axis of rotation. The integral is taken over the entire object's mass distribution.

3. What is the formula for calculating Moment of Inertia?

The formula for calculating Moment of Inertia is I = ∫r²dm, where I is the Moment of Inertia, r is the distance from the axis of rotation, and dm is the mass of an infinitesimally small element.

4. What factors affect the Moment of Inertia?

The Moment of Inertia is affected by the mass of the object, the distribution of mass around the axis of rotation, and the distance of the mass from the axis of rotation. It also depends on the shape and geometry of the object.

5. Why is calculating Moment of Inertia important?

Calculating Moment of Inertia is important because it helps in understanding an object's rotational motion and predicting how it will respond to external forces. It is also a crucial parameter in many engineering and physics applications, such as designing machines and analyzing the stability of structures.

Similar threads

Correct Use of the Parallel Axis Theorem for Moment of Inertia
    • Introductory Physics Homework Help
Replies
2
Views
624
What is the "r" in the moment of inertia?
    • Introductory Physics Homework Help
Replies
13
Views
1K
Determine the moment of inertia of a bar and disk assembly
    • Introductory Physics Homework Help
Replies
3
Views
2K
Moment of inertia of T bar about 3 axes
    • Introductory Physics Homework Help
Replies
21
Views
1K
Calculating Moment of Inertia for Hollow Cylinder w/ Water
    • Introductory Physics Homework Help
2
Replies
40
Views
2K
Moment of inertia of a rectangular prism parallel to one face
    • Introductory Physics Homework Help
Replies
11
Views
290
Solving for 'a' with Torque, Force, and Mass Moment of Inertia
    • Introductory Physics Homework Help
Replies
3
Views
858
Moment of inertia of a disk about an axis not passing through its CoM
    • Introductory Physics Homework Help
Replies
11
Views
1K
Moment of inertia of a cuboid parallel to one of its faces (repost with diagram)
    • Introductory Physics Homework Help
Replies
25
Views
455
Moment of Inertia of a sphere about an axis
    • Introductory Physics Homework Help
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top