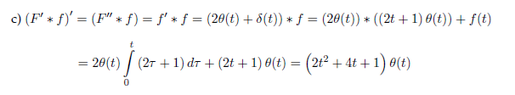goohu
- 53
- 3
I've some questions in the c) part of the task. The texts in the pictures are loosely translated, so let me know if there is something that is unclear.
View attachment 9384
Is there a specific reason why they wrote (F' * f)' instead of (f * f)' ?
I've posted a solution at the bottom of the post but I don't understand the first step: (F' * f)' = F'' * f.
Is this some standard trick that always applies?The way I would write is $$f' * f = ( 2\theta(t) + \delta(t) ) * (2t+1)\theta(t)$$, I don't see how it becomes what is written in the solution.
If someone knows of any good sources where I can read up on convolution it would be awesome if you could direct me there. Right now I only vaguely understand what convolution is (I would say: sliding two functions across each other and creating a third one by summing the overlapping area for each time unit).
I'm trying to get started on the mathematical calculations but I find it hard to grasp.
Solution:
View attachment 9385
View attachment 9384
Is there a specific reason why they wrote (F' * f)' instead of (f * f)' ?
I've posted a solution at the bottom of the post but I don't understand the first step: (F' * f)' = F'' * f.
Is this some standard trick that always applies?The way I would write is $$f' * f = ( 2\theta(t) + \delta(t) ) * (2t+1)\theta(t)$$, I don't see how it becomes what is written in the solution.
If someone knows of any good sources where I can read up on convolution it would be awesome if you could direct me there. Right now I only vaguely understand what convolution is (I would say: sliding two functions across each other and creating a third one by summing the overlapping area for each time unit).
I'm trying to get started on the mathematical calculations but I find it hard to grasp.
Solution:
View attachment 9385