RedBarchetta
- 49
- 1
Calculus: Optimization Problems
Find the area of the largest rectangle that can be inscribed in the ellipse below.
I'm not quite sure where to start...first of all, how would you even enter this into a calculator to graph? On the TI-83, I only see one variable 'x' that you can enter...
I was reading a similar problem that said this was a lagrange multiplier problem. I was never taught this method. Is there any other way to do this?
________________________________________________________________________________________________________
2. The upper right-hand corner of a piece of paper, 14 in. by 10 in., as in the figure, is folded over to the bottom edge. How would you fold it so as to minimize the length of the fold? In other words, how would you choose x to minimize y?
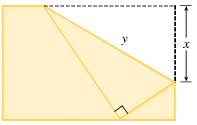
Heres what I tried to do:
First I used the pythagorean theorem. a^2+b^2=y^2
We're trying to minimize y, so I set up the distance for each side.
(14-b)=top
(10-x)=side
Plug:
(14-b)^2+(10-x)^2=y^2
Since we can't solve for two variables, solve for one. Now what would I do? or would both variables be just "x"? like:
(14-x)=top
(10-x)=side
Thanks for the help!
Homework Statement
Find the area of the largest rectangle that can be inscribed in the ellipse below.
I'm not quite sure where to start...first of all, how would you even enter this into a calculator to graph? On the TI-83, I only see one variable 'x' that you can enter...
I was reading a similar problem that said this was a lagrange multiplier problem. I was never taught this method. Is there any other way to do this?
________________________________________________________________________________________________________
2. The upper right-hand corner of a piece of paper, 14 in. by 10 in., as in the figure, is folded over to the bottom edge. How would you fold it so as to minimize the length of the fold? In other words, how would you choose x to minimize y?
Heres what I tried to do:
First I used the pythagorean theorem. a^2+b^2=y^2
We're trying to minimize y, so I set up the distance for each side.
(14-b)=top
(10-x)=side
Plug:
(14-b)^2+(10-x)^2=y^2
Since we can't solve for two variables, solve for one. Now what would I do? or would both variables be just "x"? like:
(14-x)=top
(10-x)=side
Thanks for the help!
Last edited by a moderator: