Jurgen M said:
I think you are wrong,indeed there is reduction in upwash angle that hit the wing, but not because of "induced vertical velocity", it is because of pressure loss that happened just because wing has end.
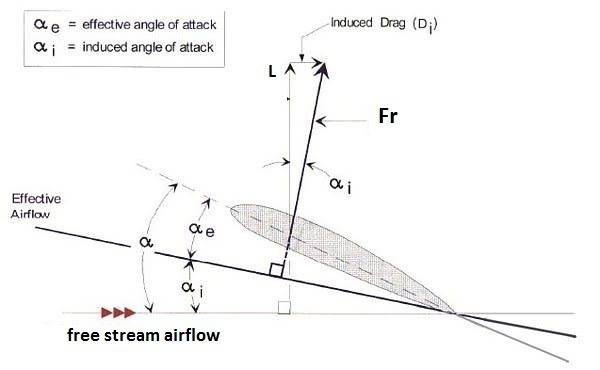
The induced downwash ahead of the wing is absolutely tied to the vorticity at the wingtips (though it's all part of a bunch of simultaneous physical principles interacting, so pointing causality just in one direction is hard to do), and the magnitude of it is exactly what we'd expect based on that formulation.
Jurgen M said:
Finite wing has pressure loss in spanwise direction,this pressure gradient cause spanwise flow. Reduction in low pressure above the leading edge reduce upwash angle.
Yes, there is a minor spanwise loss, but the majority of the pressure increase on the upper surface of a finite wing vs a 2d section is indeed because of the induced downward velocity along the wing caused by the tip vortices (well, "caused" is doing a lot of work here, it's more that there are a lot of intertwined effects that all happen because of the same overall flow physics and mathematical principles).
Jurgen M said:
Stall angle at finite wing is delayed because adverse pressure gradient is lower, it is lower because of spanwise flow/pressure loss.
Stall angle is delayed because the wing section is experiencing a locally lower angle of attack. You can see this because wing fences don't eliminate this effect.
Jurgen M said:
Induced drag theory become from equations from electromagentism, but there is nothing physical in it, vorticity in the wing wake cant induce velocity somewhere else,(in our case infront of wing)...
No, the fact that equations for flow fields have some similarities to electromagnetic field equations is just because both are continuous vector fields that follow physical laws, it's not because of trying to shoehorn in some imaginary electromagnetism here. In addition, yes, every part of the flow field absolutely can affect every other part of the flow field. That's literally the key difference between the study of subsonic and supersonic flows - in subsonic flows, disturbances can propagate both up and downstream because the disturbances can travel faster than the flow can. In supersonic flows, disturbances can only travel downstream, so nothing ahead of an object can be affected by the object.
Jurgen M said:
Listen carefully from 28:25 - 37:00
Yes, listen carefully to him around 31 minutes. Note that he shows the flowfield at a cross plane cut through the wing, and it *clearly shows* downwash between the wingtips. He doesn't disagree with me, you just don't understand what he's saying. He's not saying that the underlying math is wrong, he's saying that it's easy to have misconceptions if you don't understand how the underlying flow all works together.
Here's an exact quote from him at 32:20:
"This downwash across the span of the wing of course results in a tilting back of the lift vector, and results in what we call drag due to lift"
That's not disagreeing with me.
I honestly think he goes a bit too far in his debunking, but the core idea he has (and he's absolutely right) is that just trying to eliminate that compact vortex core at the tip is really not going to do squat to eliminate the downwash across the wing, and so there are certainly a lot of misconceptions people have, but that doesn't change that the vortices and associated downwash absolutely exist (and as I said, you can get in a bit of a quibble about what "causes" what, since it's all tied together in a bunch of simultaneous PDEs).