SUMMARY
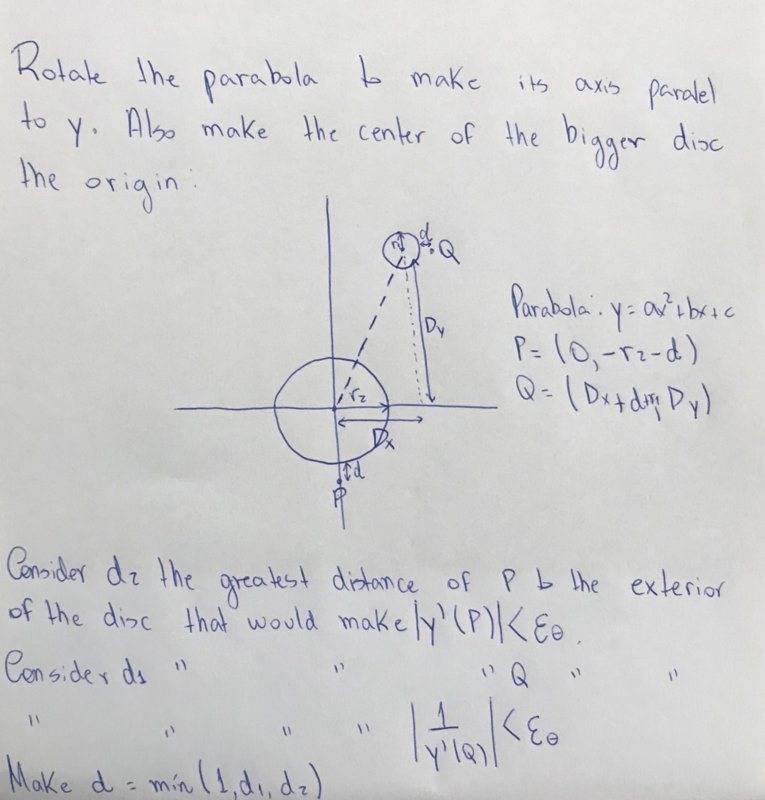
The discussion centers on a mathematical problem involving two disks in a plane and the intersection of parabolas. The proposed solution asserts that by selecting two points exterior to the disks, one can ensure that all parabolas passing through these points will intersect at least one of the disks. The reasoning provided highlights that no two points on a parabola share the same slope, thus making it impossible for a parabola to be tangent to both points on the disks simultaneously. However, slight movements away from the disks could allow for parabolas to avoid intersection, indicating a delicate balance in the problem's conditions.
PREREQUISITES
- Understanding of basic geometry, specifically properties of parabolas and circles.
- Familiarity with the concept of tangents and slopes in calculus.
- Knowledge of mathematical proof techniques, particularly in geometry.
- Ability to visualize geometric configurations in a plane.
NEXT STEPS
- Explore the properties of parabolas and their intersections with circles.
- Study geometric proof techniques, focusing on problems involving tangents and slopes.
- Investigate the implications of moving points in geometric configurations.
- Learn about advanced topics in plane geometry, such as theorems related to conic sections.
USEFUL FOR
Mathematicians, geometry enthusiasts, educators, and students seeking to deepen their understanding of geometric relationships and proof strategies involving curves and shapes.