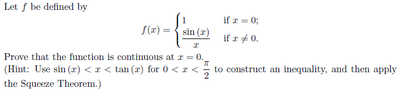Can Dividing by Sin x Help Prove Continuity at x = 0?

  • Context: MHB 
  • Thread starter Thread starter Joe20
  • Start date Start date
  • Tags Tags
    Continuous Proof
Click For Summary
SUMMARY

The discussion centers on the mathematical approach to proving continuity at x = 0 by dividing by sin x. Participants suggest that utilizing the hint provided in the problem, which involves dividing by sin x, is a more appropriate method. This technique aligns with established mathematical principles and can effectively demonstrate the continuity of functions at the specified point.

PREREQUISITES
  • Understanding of limits in calculus
  • Familiarity with the properties of the sine function
  • Knowledge of continuity in mathematical functions
  • Basic algebraic manipulation skills
NEXT STEPS
  • Study the limit properties of sin x as x approaches 0
  • Explore the epsilon-delta definition of continuity
  • Learn about L'Hôpital's Rule for indeterminate forms
  • Investigate the Taylor series expansion of sin x
USEFUL FOR

Students and educators in calculus, mathematicians focusing on continuity proofs, and anyone seeking to deepen their understanding of trigonometric limits.

Joe20
Messages
53
Reaction score
1
Not sure how to do this question. Help needed. Thanks
 

Attachments

  • 3.png
    3.png
    7 KB · Views: 126
Physics news on Phys.org
Another hint:
Use the well-known result $\displaystyle\lim_{x\to0}\frac{\sin x}x=1$.
 
Olinguito said:
Another hint:
Use the well-known result $\displaystyle\lim_{x\to0}\frac{\sin x}x=1$.


Given the hint that comes with the problem, I wouldn't think that would be appropriate. Alternatively one might suggest dividing everything by $\sin x$, which seems more in line with the hint.
 

Similar threads

MHB Prove/Disprove: Uniform Continuity of sin(sin(x))
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Proving a function f is continuous given A U B = X
  • · Replies 5 ·
Replies
5
Views
3K
MHB Continuity of f^+ .... Browder Corollary 3.13
  • · Replies 4 ·
Replies
4
Views
2K
MHB Proof that Arcsin x is continuous ....
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad Continuity of f^+ .... Browder Corollary 3.13
  • · Replies 18 ·
Replies
18
Views
2K
Graduate Question about existence of path-lifting property
  • · Replies 8 ·
Replies
8
Views
2K
Undergrad Understanding an argument in Intermediate Value Theorem
  • · Replies 5 ·
Replies
5
Views
3K
MHB Compactness and Continuity in R^n .... .... D&K Theorem 1.8.8 .... ....
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Definitions of Continuity in Topological Spaces ....
  • · Replies 2 ·
Replies
2
Views
3K
MHB Composition of Two Continuous Functions .... Browder, Proposition 3.12 .... ....
  • · Replies 2 ·
Replies
2
Views
2K